题目内容
已知函数![]() (1)若
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;(2)若定义在区间D上的函数
的取值范围;(2)若定义在区间D上的函数![]() 对于区间
对于区间![]() 上的任意两个值
上的任意两个值![]() 总有以下不等式
总有以下不等式![]() 成立,则称函数
成立,则称函数![]() 为区间
为区间![]() 上的
上的
“凹函数”.试证:当![]() 时,
时,![]() 为“凹函数”.
为“凹函数”.
解(1)由![]() ,得
,得![]() ……………………2分
……………………2分
函数为![]() 上单调函数. 若函数为
上单调函数. 若函数为![]() 上单调增函数,则
上单调增函数,则![]() 在
在![]() 上恒成立,即不等式
上恒成立,即不等式![]() 在
在![]() 上恒成立. 也即
上恒成立. 也即![]() 在
在![]() 上恒成立. …………4分令
上恒成立. …………4分令![]() ,上述问题等价于
,上述问题等价于![]() ,而
,而![]() 为在
为在![]() 上的减函数,则
上的减函数,则![]() ,于是
,于是![]() 为所求. …………6分
为所求. …………6分
(2)证明:由![]() 得
得

![]() ………………………7分
………………………7分
 ……………………8分
……………………8分
而![]() ① ………………10分
① ………………10分
又![]() , ∴
, ∴![]() ② ………11分
② ………11分
∵![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ③ ……………………………13分
③ ……………………………13分
由①、②、③得
即![]() ,从而由凹函数的定义可知函数为凹函数. …………14分
,从而由凹函数的定义可知函数为凹函数. …………14分

练习册系列答案
相关题目
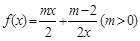 .
.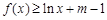 在
在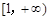 上恒成立,求m取值范围;
上恒成立,求m取值范围;
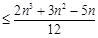 (
(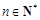 ).
).
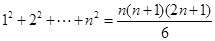 )
)
 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围; 对于区间
对于区间 上的任意两个值
上的任意两个值 总有以下不等式
总有以下不等式 成立,则称函数
成立,则称函数 时,
时,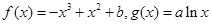 .
.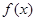 在
在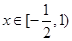 上的最大值为
上的最大值为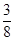 ,求实数
,求实数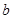 的值;
的值;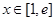 ,都有
,都有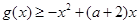 恒成立,求实数
恒成立,求实数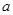 的取值范围;
的取值范围;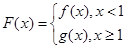 ,对任意给定的正实数
,对任意给定的正实数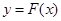 上是否存在两点
上是否存在两点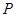 、
、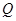 ,使得
,使得 是以
是以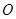 (
(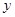 轴上?请说明理由。
轴上?请说明理由。 .
. 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围; 是
是 上的最小值和最大值.
上的最小值和最大值.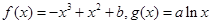 .
.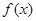 在
在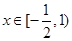 上的最大值为
上的最大值为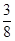 ,求实数
,求实数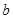 的值;
的值;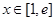 ,都有
,都有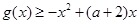 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;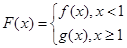 ,对任意给定的正实数
,对任意给定的正实数 上是否存在两点
上是否存在两点 、
、 ,使得
,使得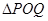 是以
是以 (
( 轴上?请说明理由。
轴上?请说明理由。