题目内容
(2012•唐山二模)曲线y=
在点(0,-1)处的切线与两坐标轴围成的封闭图形的面积为( )
| x-1 |
| x+1 |
分析:先求切线方程,再求切线与两坐标轴的交点坐标,即可求得切线与两坐标轴围成的封闭图形的面积
解答:解:求导函数,可得y′=
,当x=0时,y′=2,
∴曲线y=
在点(0,一1)处的切线方程为y=2x-1,
∴当y=0时,x=
∴切线与两坐标轴的交点坐标为(
,0),(0,-1)
∴所求面积为
×
×1=
故选C.
| 2 |
| (x+1)2 |
∴曲线y=
| x-1 |
| x+1 |
∴当y=0时,x=
| 1 |
| 2 |
∴切线与两坐标轴的交点坐标为(
| 1 |
| 2 |
∴所求面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故选C.
点评:本题考查导数的几何意义,考查切线方程,考查三角形面积的计算,属于基础题.

练习册系列答案
相关题目
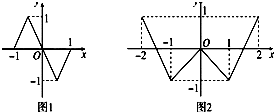 (2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )
(2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )