题目内容
已知函数f(x)=ex-ax-1(a∈R).
(1)讨论f(x)=ex-ax-1(a∈R)的单调性;
(2)若a=1,求证:当x≥0时,f(x)≥f(-x).
(1)解:f′(x)=ex-a.当a≤0时,f′(x)≥0恒成立,
当a>0时,令f′(x)>0, 得x>ln a;令f′(x)<0,得x<ln a.
得x>ln a;令f′(x)<0,得x<ln a.
综上,当a≤0时,f(x)在(-∞,+∞)上单调递增;
当a>0时,增区间是(ln a,+∞),减区间是(-∞,ln a).----------6分
(2)证明:令g(x)=f(x)-f(-x)=ex- -2x,g′(x)=ex+e-x-2≥0,
-2x,g′(x)=ex+e-x-2≥0,
∴g(x)在[0,+∞)上是增函数,∴g(x)≥g( 0)=0,
0)=0,
∴f(x)≥f(-x).------------12分

练习册系列答案
相关题目
 中,
中, ,
,
 ,设
,设 .
. 是等比数列;
是等比数列; 的前
的前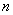 项和
项和 ;
; ,
, 为数列
为数列 的前
的前 的最大的整数.
的最大的整数. 、
、 的夹角为
的夹角为 ,且
,且 ,
, ,则向量
,则向量 的夹角等于 .
的夹角等于 . 的解集为
的解集为 ,那么函数
,那么函数 的大致图象是( )
的大致图象是( )
 >
> ,则a<b;
,则a<b; {1,2,3,4,5},A
{1,2,3,4,5},A .
. ≤y≤
≤y≤ ,N=
,N= ≥
≥ ,则表示M∩N的图形面积等于 .
,则表示M∩N的图形面积等于 .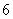 点到
点到 点之间在食堂见面,先到之人等后到之人十五分
点之间在食堂见面,先到之人等后到之人十五分