题目内容
12.在△ABC中,角A,B,C所对的边分别为a,b,c,且$\sqrt{3}a$=2csinA.(1)求角C的大小;
(2)若△ABC为锐角三角形,且c=2,且a+b=3,求△ABC的面积.
分析 (1)由正弦定理化简已知等式可得2sinCsinA=$\sqrt{3}$sinA,又sinA≠0,解得sinC=$\frac{\sqrt{3}}{2}$,结合范围C∈(0,π),即可求C的值.
(2)由余弦定理可得:4=a2+b2-2abcosC=(a+b)2-3ab=9-3ab,解得ab=$\frac{5}{3}$,根据三角形面积公式即可得解.
解答 解:(1)∵由正弦定理可得2sinCsinA=$\sqrt{3}$sinA,sinA≠0,即有sinC=$\frac{\sqrt{3}}{2}$,
∴由C∈(0,π),则C=$\frac{π}{3}$或$\frac{2π}{3}$.
(2)∵△ABC为锐角三角形,
∴C=$\frac{π}{3}$,c=2,且a+b=3,
∴由余弦定理可得:4=a2+b2-2abcosC=(a+b)2-3ab=9-3ab,解得:ab=$\frac{5}{3}$,
∴${S}_{△ABC}=\frac{1}{2}$absinC=$\frac{1}{2}×$$\frac{5}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{12}$.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式的应用,考查了正弦函数的图象和性质,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
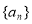 的前
的前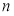 项和记为
项和记为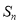 ,
, ,
,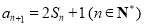 .
.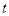 为何值时,数列
为何值时,数列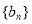 的前
的前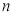 项和
项和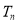 有最大值,且
有最大值,且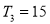 ,
, ,
,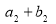 ,
, 成等比数列,求
成等比数列,求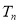 .
.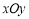 中,设直线
中,设直线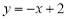 与圆
与圆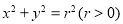 交于
交于 两点,
两点,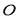 为坐标原点,若圆上一点
为坐标原点,若圆上一点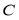 满足
满足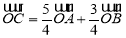 ,则
,则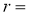
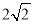 B.
B. C.
C. D.
D.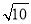
 上的函数
上的函数 满足
满足 且
且 时,
时, 则
则 __________.
__________.