题目内容
定义域为R的连续函数 ,对任意x都有
,对任意x都有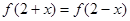 ,且其导函数
,且其导函数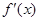 满足
满足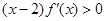 ,则当
,则当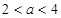 时,有( )
时,有( )
A.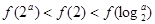 B.
B.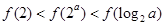
C.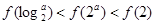 D.
D.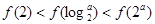
【答案】
D
【解析】
试题分析:∵对任意 都有
都有 ,∴
,∴ 是
是 的对称轴,又∵
的对称轴,又∵ ,∴当
,∴当 时,
时, ,
, 是增函数;当
是增函数;当 时,
时, ,
, 是减函数;又∵
是减函数;又∵ ,∴
,∴ ,
, ;由
;由 ,得
,得 ,∴
,∴ ,由
,由 ,得
,得 ,∴
,∴ ;∴
;∴ ,∴
,∴ ,即
,即 ,故选:D.
,故选:D.
考点:利用导数研究函数的单调性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目