题目内容
设全集U={(x,y)|x,y∈R},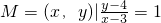 ,N={(x,y)|y≠x+1},那么(CUM)∩(CUN)=
,N={(x,y)|y≠x+1},那么(CUM)∩(CUN)=
- A.∅
- B.{(3,4)}
- C.(3,4)
- D.{(x,y)|y≠x+1}
B
分析:全集U={(x,y)|x,y∈R}表示整个坐标平面,由集合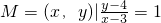 表示直线y-4=x-3,但去掉点(3,4),知CUM表示整个平面去掉直线y-4=x-3,但补上点(3,4).由集合N={(x,y)|y≠x+1}表示整个平面去掉直线y=x+1,知CUN表示直线y=x+1,由此能求出(CUM)∩(CUN).
表示直线y-4=x-3,但去掉点(3,4),知CUM表示整个平面去掉直线y-4=x-3,但补上点(3,4).由集合N={(x,y)|y≠x+1}表示整个平面去掉直线y=x+1,知CUN表示直线y=x+1,由此能求出(CUM)∩(CUN).
解答:全集U={(x,y)|x,y∈R}表示整个坐标平面,
∵集合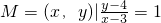 表示直线y-4=x-3,但去掉点(3,4),
表示直线y-4=x-3,但去掉点(3,4),
∴CUM表示整个平面去掉直线y-4=x-3,但补上点(3,4).
∵集合N={(x,y)|y≠x+1}表示整个平面去掉直线y=x+1,
∴CUN表示直线y=x+1,
故(CUM)∩(CUN)={(3,4)}.
故选B.
点评:本题考查集合的交、并、补集的混合运算,是基础题.解题时要认真审题,仔细解答.
分析:全集U={(x,y)|x,y∈R}表示整个坐标平面,由集合
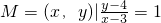 表示直线y-4=x-3,但去掉点(3,4),知CUM表示整个平面去掉直线y-4=x-3,但补上点(3,4).由集合N={(x,y)|y≠x+1}表示整个平面去掉直线y=x+1,知CUN表示直线y=x+1,由此能求出(CUM)∩(CUN).
表示直线y-4=x-3,但去掉点(3,4),知CUM表示整个平面去掉直线y-4=x-3,但补上点(3,4).由集合N={(x,y)|y≠x+1}表示整个平面去掉直线y=x+1,知CUN表示直线y=x+1,由此能求出(CUM)∩(CUN).解答:全集U={(x,y)|x,y∈R}表示整个坐标平面,
∵集合
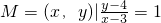 表示直线y-4=x-3,但去掉点(3,4),
表示直线y-4=x-3,但去掉点(3,4),∴CUM表示整个平面去掉直线y-4=x-3,但补上点(3,4).
∵集合N={(x,y)|y≠x+1}表示整个平面去掉直线y=x+1,
∴CUN表示直线y=x+1,
故(CUM)∩(CUN)={(3,4)}.
故选B.
点评:本题考查集合的交、并、补集的混合运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 },B={x|y=ln(1-2x)}.
},B={x|y=ln(1-2x)}.