题目内容
函数 的零点个数是 ( )
的零点个数是 ( )
| A.0个 | B.1个 | C.2个 | D.3个 |
D
解析考点:函数零点的判定定理.
专题:作图题;数形结合;方程思想;转化思想.
分析:本题考查的是函数零点的个数判定问题.在解答时,可先结合函数的特点将问题转化为研究两个函数图象交点的问题.继而问题可获得解答.
解答:
解:由题意可知:要研究函数 的零点个数,只需研究函数y=2
的零点个数,只需研究函数y=2 ,y= x
,y= x 的图象交点个数即可.
的图象交点个数即可.
画出函数y=2 ,y= x
,y= x 的图象
的图象
由图象可得有3个交点.
故选D.
点评:本题考查的是函数零点的个数判定问题.在解答的过程当中充分体现了函数与方程的思想、数形结合的思想以及问题转化的思想.值得同学们体会和反思.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
已知幂函数 的图像经过点(2,4),则下列命题中不正确的是( )
的图像经过点(2,4),则下列命题中不正确的是( )
| A.函数图像过点(-1,1) | B.当 时,函数 时,函数 取值范围是 取值范围是 |
C. | D.函数 单调减区间为 单调减区间为 |
(09江西改编)已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 的值为
的值为
A. | B. | C. | D. |
设定义域为R的函数 ,则关于
,则关于 的方程
的方程 有7个不同实数解的充要条件是( )
有7个不同实数解的充要条件是( )
A. 且 且 | B. 且 且 |
C. 且 且 | D. 且 且 |
已知 是R上的偶函数,若
是R上的偶函数,若 的图象向右平移一个单位后,则得到一
的图象向右平移一个单位后,则得到一
个奇函数的图象,w则 的值为( )
的值为( )
| A.1 | B.0 | C.-1 | D. |
定义在R上的偶函数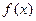 在
在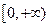 上递增,
上递增,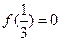 ,则满足
,则满足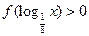 的
的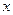 的取值范围是( )
的取值范围是( )
A.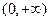 | B.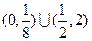 | C.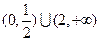 | D.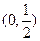 |
定义在R上的偶函数 在
在 上是增函数,且具有性质:
上是增函数,且具有性质: ,则该函数( )
,则该函数( )
A.在 上是增函数 上是增函数 | B.在 上是增函数在 上是增函数在 上是减函数 上是减函数 |
C.在 上是减函数 上是减函数 | D.在 上是减函数在 上是减函数在 上是增函数 上是增函数 |
函数f(x)=log2x-x+2的零点个数为( )
| A.0 | B.1 |
| C.2 | D.3 |
 是定义在R上的偶函数,
是定义在R上的偶函数, ,
, 的解集为 ( )
的解集为 ( )