题目内容
2.函数y=x3(x>0)的图象在点(ak,ak3)处的切线所对应的一次函数的零点为ak+1,其中k∈N*.若a1=2,则a1+a3+a5的值是$\frac{266}{81}$.分析 先求出函数y=x3(x>0)在点(ak,ak3)处的切线方程,再求出切线方程的零点ak+1,
根据数列{an}的特征,计算出a1+a3+a5的值.
解答 解:∵y=x3(x>0),
∴y′=3x2,
∴y=x3(x>0)在点(ak,ak3)处的切线方程是:
y-ak3=3${{a}_{k}}^{2}$(x-ak),
整理得,3${{a}_{k}}^{2}$x-y-2ak3=0;
又∵切线方程的零点为ak+1,
∴ak+1=$\frac{2}{3}$ak,
∴{an}是首项为a1=2,公比q=$\frac{2}{3}$的等比数列,
∴a1+a3+a5=2+2×$\frac{4}{9}$+2×$\frac{16}{81}$=$\frac{266}{81}$.
故答案为:$\frac{266}{81}$.
点评 本题考查了利用导数求函数在某一点处的切线方程的应用问题,也考查了等比数列的应用问题,解题时应注意导数、切线方程和等比数列性质的灵活运用.

练习册系列答案
相关题目
13.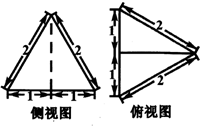 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
10.将函数f(x)=sin(2x-$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{3}$个单位(纵坐标不变),则所得图象的解析式是( )
| A. | y=-cos2x | B. | y=cos2x | C. | y=sin(2x-$\frac{5π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |
17.图中所示算法流程图的功能是( )


| A. | 求a、b、c三数的最大数 | B. | 求a、b、c三数的最小数 | ||
| C. | 将a、b、c三数由大到小排列 | D. | 将a、b、c三数由小到大排列 |
7.已知各项均为正数的等比数列{an}中,a2=1,则其前3项的和S3的取值范围是( )
| A. | (1,+∞) | B. | (0,2] | C. | (0,3] | D. | [3,+∞) |
14.已知点P(x,y)是直线x+3y-2=0上的动点,则代数式2x+3×8y有( )
| A. | 最小值2$\sqrt{3}$ | B. | 最大值2$\sqrt{3}$ | C. | 最小值4$\sqrt{3}$ | D. | 最大值4$\sqrt{3}$ |
11.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,交y轴于点P,若|OF|=2|OP|,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
12.设向量$\overline a=(1,2),\overrightarrow b=(m,m+1),\overrightarrow a⊥\overrightarrow b$,则实数m的值为( )
| A. | 0 | B. | -$\frac{2}{3}$ | C. | -$\frac{9}{5}$ | D. | -3 |
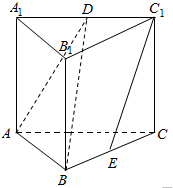 直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.
直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.