题目内容
【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 的零点个数;
的零点个数;
(Ⅱ)若![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)1;(Ⅱ) ![]() .
.
【解析】试题分析:
(1)由导函数结合函数的极值可得函数![]() 在
在![]() 内有且只有一个零点;
内有且只有一个零点;
(2) 构造函数![]() ,
,
若![]() ,不符合题意,讨论
,不符合题意,讨论![]() 可得
可得![]() ,
,
二次构造函数![]() ,结合函数的性质可得
,结合函数的性质可得![]() 的最大值为
的最大值为![]() .
.
试题解析:
(Ⅰ)当![]() 时,
时, ![]() ,定义域为
,定义域为![]() ,
,
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 内无零点;
内无零点;
当![]() 时,
时, ![]() ,因为
,因为![]() ,
, ![]() ,所以
,所以![]() ,说明函数
,说明函数![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,当
,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 内有且只有一个零点;
内有且只有一个零点;
综上,函数![]() 的零点个数是1;
的零点个数是1;
(Ⅱ)若![]() ,即
,即![]() ,设
,设![]() ,
,
若![]() ,则当
,则当![]() 时,显然
时,显然![]() ,故不符合题意,所以
,故不符合题意,所以![]() .
.
![]() (
(![]() ),
),
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
从而![]() ,
,
由题意可知![]() ,所以
,所以![]() ,
,
此时![]() ,令
,令![]() ,
, ![]() ,
,
可知![]() 在
在![]() 上单调增,在
上单调增,在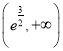 上单调减,
上单调减,
所以![]() ,故
,故![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
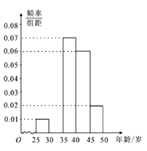
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.