题目内容
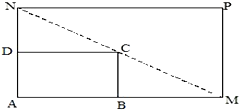 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=2米,AD=1米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=2米,AD=1米.(1)设BM=x(单位:米),要使花坛AMPN的面积大于9平方米,求x的取值范围;
(2)若x∈[1,3](单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积.
分析:(1)由三角形相似得到AN与x的关系,然后直接代入矩形面积公式,最后求解一元二次不等式即可得到答案;
(2)由函数f(x)=x+
+4,x∈[1,3],的单调性可求得结论.
(2)由函数f(x)=x+
| 4 |
| x |
解答:解:(1)设花坛AMPN的面积为f(x),
由
=
,∴AN=
,∴f(x)=
(x>0).
要使花坛面积大于9,即
>9,解得0<x<1或x>4;
(2)由f(x)=
(x>0).
则f(x)=x+
+4,x∈[1,3],
因为f(x)在[1,2]上递减,在(2,3]上递增,
又f(1)=9,f(3)=
,
所以当x=1时,fmax(x)=9,
即当AM=3米,AN=3米时,花坛AMPN面积最大为9平方米.
由
| x |
| 2+x |
| 1 |
| AN |
| 2+x |
| x |
| (2+x)2 |
| x |
要使花坛面积大于9,即
| (2+x)2 |
| x |
(2)由f(x)=
| (2+x)2 |
| x |
则f(x)=x+
| 4 |
| x |
因为f(x)在[1,2]上递减,在(2,3]上递增,
又f(1)=9,f(3)=
| 25 |
| 3 |
所以当x=1时,fmax(x)=9,
即当AM=3米,AN=3米时,花坛AMPN面积最大为9平方米.
点评:本题考查了根据实际问题选择函数模型,考查了不等式的解法,考查了函数y=x+
(k>0)的单调性,是中档题.
| k |
| x |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)