题目内容
设面积为S的平面四边形的第i条边的边长为ai(i=1,2,3,4),P是该四边形内一点,点P到第i条边的距离记为hi,若
=
=
=
=k,则
(ihi=
),类比上述结论,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),Q是该三棱锥内的一点,点Q到第i个面的距离记为di,若
=
=
=
=k,则
(idi)等于______.
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
| 4 |
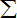 |
| i=1 |
| 2S |
| k |
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S4 |
| 4 |
| 4 |
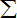 |
| i=1 |
根据三棱锥的体积公式 V=
Sh
得:
S1H1+
S2H2+
S3H3+
S4H4=V,
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4=
,
即
(iHi)=
.
故答案为:
.
| 1 |
| 3 |
得:
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4=
| 3V |
| K |
即
| 4 |
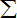 |
| i=1 |
| 3V |
| K |
故答案为:
| 3V |
| k |

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目



 ,这与三角形内角和为
,这与三角形内角和为 相矛盾,
相矛盾, 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角 、
、 、
、 中有两个直角,不妨设
中有两个直角,不妨设