题目内容
已知 为奇函数(a,b是常数),且函数f(x)的图象过点
为奇函数(a,b是常数),且函数f(x)的图象过点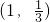
(1)求f(x)的表达式;
(2)定义正数数列{an}, ,求数列{an2}的通项公式;
,求数列{an2}的通项公式;
(3)已知 ,设Sn为bn的前n项和,证明:
,设Sn为bn的前n项和,证明: .
.
解:(1) 为奇函数
为奇函数
∴ ,
,
∴a=0
又f(x)过点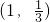 ,
,
∴ ,∴b=1
,∴b=1
∴
(2)∵
∴ ∴
∴
∴数列 是以2为首项,
是以2为首项, 为公比的等比数列
为公比的等比数列
∴ ∴
∴
(3)由(2)知:
∴
∵
∴
分析:(1)根据所给的函数是一个奇函数,根据奇函数的定义,得到a的值,根据函数过一个定点,把点的坐标代入,利用待定系数法得到结果.
(2)根据条件写出数列的递推式,下面整理数列,通过配凑整理出数列 是以2为首项,
是以2为首项, 为公比的等比数列,写出数列通项,变形整理出结果.
为公比的等比数列,写出数列通项,变形整理出结果.
(3)根据条件写出新数列的通项,观察新数列分母的结构,整理出可以应用裂项的方法来解题,用裂项做出数列的前n项和,利用分析法写出要证的不等式.
点评:本题考查数列和函数的综合,本题解题的关键是构造正确的新函数,判断出所给的数列是一个特殊的数列,本题是一个可以作为压轴题目出现的题目.
 为奇函数
为奇函数∴
 ,
,∴a=0
又f(x)过点
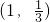 ,
,∴
 ,∴b=1
,∴b=1∴

(2)∵

∴
 ∴
∴
∴数列
 是以2为首项,
是以2为首项, 为公比的等比数列
为公比的等比数列 ∴
 ∴
∴
(3)由(2)知:

∴

∵

∴

分析:(1)根据所给的函数是一个奇函数,根据奇函数的定义,得到a的值,根据函数过一个定点,把点的坐标代入,利用待定系数法得到结果.
(2)根据条件写出数列的递推式,下面整理数列,通过配凑整理出数列
 是以2为首项,
是以2为首项, 为公比的等比数列,写出数列通项,变形整理出结果.
为公比的等比数列,写出数列通项,变形整理出结果.(3)根据条件写出新数列的通项,观察新数列分母的结构,整理出可以应用裂项的方法来解题,用裂项做出数列的前n项和,利用分析法写出要证的不等式.
点评:本题考查数列和函数的综合,本题解题的关键是构造正确的新函数,判断出所给的数列是一个特殊的数列,本题是一个可以作为压轴题目出现的题目.

练习册系列答案
相关题目
 为奇函数(a,b是常数),且函数f(x)的图象过点
为奇函数(a,b是常数),且函数f(x)的图象过点
 ,求数列{an2}的通项公式;
,求数列{an2}的通项公式; ,设Sn为bn的前n项和,证明:
,设Sn为bn的前n项和,证明: .
. 为奇函数(a,b是常数),且函数f(x)的图象过点
为奇函数(a,b是常数),且函数f(x)的图象过点
 ,求数列{an2}的通项公式;
,求数列{an2}的通项公式; ,设Sn为bn的前n项和,证明:
,设Sn为bn的前n项和,证明: .
.