题目内容
函数f(x)=x-tanx (-
<x<
)的零点个数为
______.
| π |
| 2 |
| π |
| 2 |
因为函数f(x)=x-tanx (-
<x<
)的零点就是函数图象与x轴的交点的横坐标.
又y'=1-
=
,当x=0时,y'=0,且y=0.
当-
<x<0时,y'<0,所以原函数递减
当0<x<
时,y'<0,原函数递减
故函数f(x)=x-tanx (-
<x<
)是减函数.又因为当x=0时y=0.所以函数只有一个零点 0.
故答案为:1.
| π |
| 2 |
| π |
| 2 |
又y'=1-
| 1 |
| cos 2x |
| cos 2x-1 |
| cos 2x |
当-
| π |
| 2 |
当0<x<
| π |
| 2 |
故函数f(x)=x-tanx (-
| π |
| 2 |
| π |
| 2 |
故答案为:1.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 ,3),N(
,3),N( 个单位得到函数g(x)图象,直线x=t(t∈[0,
个单位得到函数g(x)图象,直线x=t(t∈[0, ])与f(x),g(x)的图象分别交于P,Q两点,求|PQ|的最大值.
])与f(x),g(x)的图象分别交于P,Q两点,求|PQ|的最大值.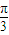 ,3),N(
,3),N(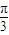 ,-3).
,-3).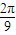 个单位得到函数g(x)图象,直线x=t(t∈[0,
个单位得到函数g(x)图象,直线x=t(t∈[0,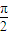 ])与f(x),g(x)的图象分别交于P,Q两点,求|PQ|的最大值.
])与f(x),g(x)的图象分别交于P,Q两点,求|PQ|的最大值. ,3),N(
,3),N( ,-3).
,-3).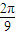 个单位得到函数g(x)图象,直线x=t(t∈[0,
个单位得到函数g(x)图象,直线x=t(t∈[0,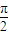 ])与f(x),g(x)的图象分别交于P,Q两点,求|PQ|的最大值.
])与f(x),g(x)的图象分别交于P,Q两点,求|PQ|的最大值.