题目内容
已知向量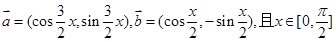 ,
,
(1)求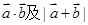 ;
;
(2)若 的最小值是
的最小值是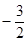 ,求实数
,求实数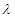 的值.
的值.
(1) ,
,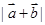 =2cosx(2)
=2cosx(2)
解析试题分析:(1)由向量的坐标运算,利用公式化简即可;(2)原函数由向量坐标运算可化为 即
即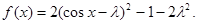 又最小值
又最小值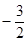 ,则结合二次函数最值可求得
,则结合二次函数最值可求得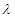 .
.
试题解析:解:(1)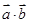 =
=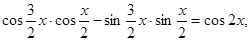
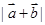 =
= ,
,
∵ ,∴
,∴
∴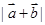 =2cosx. 6分
=2cosx. 6分
(2)由(1)得
即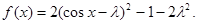
∵ ,∴
,∴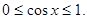
 时,当且仅当
时,当且仅当 取得最小值-1,这与已知矛盾.
取得最小值-1,这与已知矛盾.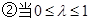 时,当且仅当
时,当且仅当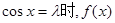 取最小值
取最小值
由已知得 ,解得
,解得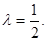
 时,当且仅当
时,当且仅当 取得最小值
取得最小值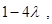
由已知得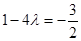 ,解得
,解得 ,这与
,这与 相矛盾.
相矛盾.
综上所述, 为所求. 12分
为所求. 12分
考点:向量的坐标运算,二次函数求最值,函数与方程的数学思想,分类讨论的数学思想.

练习册系列答案
相关题目
已知数列2,5,11,20,x,47, 合情推出x的值为( )
| A.29 | B.31 | C.32 | D.33 |
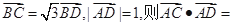 ________.
________. 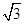 cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+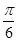 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n. ·
· =
=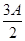 ,sin
,sin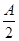 ,sin
,sin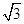 .
.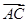 |+|
|+| |=
|=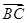 |,试判断△ABC的形状.
|,试判断△ABC的形状.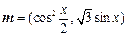 ,
,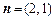 ,函数
,函数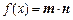 .
.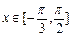 时,求函数
时,求函数 的取值范围;
的取值范围;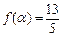 ,且
,且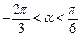 时,求
时,求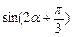 的值.
的值.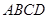 中,
中,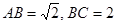 ,点
,点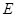 是
是 边的中点,点
边的中点,点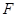 在边
在边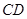 上.
上. 是对角线
是对角线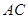 的中点,
的中点, 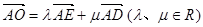 ,求
,求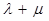 的值;
的值;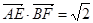 ,求线段
,求线段 的长.
的长.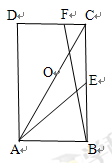
 -t
-t )·
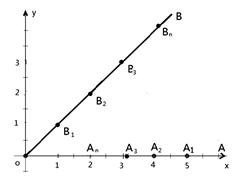
)· 为原点,射线
为原点,射线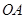 与
与 轴正半轴重合,射线
轴正半轴重合,射线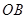 是第一象限角平分线.在
是第一象限角平分线.在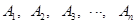 ,
,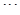 ,在
,在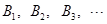 ,
,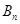 ,
,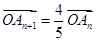 ,
,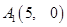 ,
,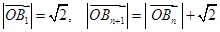 .
.
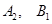 的坐标;
的坐标;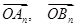 的坐标;
的坐标; 面积的最大值,并说明理由.
面积的最大值,并说明理由.