题目内容
在平面α内有一个正△ABC，以BC边为轴把△ABC旋转θ角，θ∈（0，
），得到△A'BC，当cosθ=______时，△A'BC在平面α内的射影是直角三角形．
| π |
| 2 |
取BC的中点D，连接AD，A′D，如下图所示
∵△ABC为正三角形，则△A'BC为等腰直角三角形
则AD⊥BC，A′D⊥BC
∴∠ADA′=θ
设△ABC的边长为a，
则在Rt△ADA′中，AD=
a，A′D=
故cosθ=cos∠ADA′=
故答案为：
∵△ABC为正三角形，则△A'BC为等腰直角三角形
则AD⊥BC，A′D⊥BC
∴∠ADA′=θ
设△ABC的边长为a，
则在Rt△ADA′中，AD=
| ||
| 2 |
| a |
| 2 |
故cosθ=cos∠ADA′=
| ||
| 3 |
故答案为：
| ||
| 3 |
练习册系列答案
相关题目
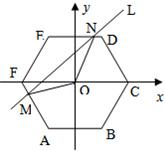如图，在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF，AB∥Ox．直线L：y=kx+t（k为常数）与正六边形交于M、N两点，记△OMN的面积为S，则函数S=f（t）的奇偶性为（ ）| A、偶函数 | B、奇函数 | C、不是奇函数，也不是偶函数 | D、奇偶性与k有关 |
），得到△A'BC，当cosθ= 时，△A'BC在平面α内的射影是直角三角形．
），得到△A'BC，当cosθ= 时，△A'BC在平面α内的射影是直角三角形．