题目内容
（2013•未央区三模）（几何证明选讲）以Rt△ABC的直角边AB为直径的圆O交AC边于点E，点D在BC上，且DE与圆O相切．若∠A=56°，则∠BDE=
68°
68°
．分析：已知∠A=56°，利用外角定理可得∠BOE=112°，因为∠ABC=90°，DE与圆O相切，可得O、B、C、E四点共圆，利用其性质即可得到∠BDE．
解答：解：连接OE，因为∠A=56°，所以∠BOE=112°，
又因为∠ABC=90°，DE与圆O相切，
所以O、B、C、E四点共圆，
所以∠BDE=180°-∠BOE=68°．
故答案为68°．
又因为∠ABC=90°，DE与圆O相切，
所以O、B、C、E四点共圆，
所以∠BDE=180°-∠BOE=68°．
故答案为68°．
点评：熟练掌握三角形的外角定理、圆的切线的性质、O、B、C、E四点共圆的判定与性质是解题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
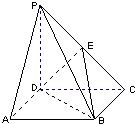（2013•未央区三模）如图，四棱锥P-ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．
（2013•未央区三模）某三棱锥的三视图如图所示，该三棱锥的体积是为（ ）