题目内容
已知函数f（x）=sin（2x+φ）（-π＜φ＜0），且其图象的一条对称轴是直线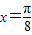
，（1）求φ的值；
（2）求函数f（x）的单调递增区间．
【答案】分析：（1）根据其图象的一条对称轴是直线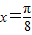
，结合-π＜φ＜0，求出φ的值．
由（1）求出函数的解析式，利用正弦函数的单调增区间，求出函数的单调增区间．
解答：解：（1）∵x=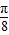
是函数图象的一条对称轴，∴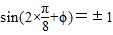
∴
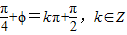，∵-π＜ϕ＜0，∴
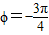．（4分）
（2）由（1）知ϕ=-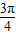
，∴
，
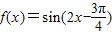由题意得kπ+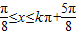
，k∈Z
故函数函数f（x）的单调递增区间是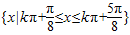
，k∈Z（8分）
点评：本题是基础题，考查三角函数的基本性质，函数的对称性，单调性，掌握基本函数的基本性质，是学好数学的关键．
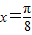，结合-π＜φ＜0，求出φ的值．由（1）求出函数的解析式，利用正弦函数的单调增区间，求出函数的单调增区间．
解答：解：（1）∵x=
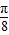是函数图象的一条对称轴，∴∴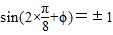
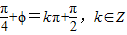，∵-π＜ϕ＜0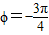，∴．（4分）（2）由（1）知ϕ=-
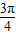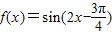，∴，由题意得kπ+
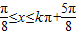，k∈Z故函数函数f（x）的单调递增区间是
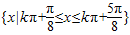，k∈Z（8分）点评：本题是基础题，考查三角函数的基本性质，函数的对称性，单调性，掌握基本函数的基本性质，是学好数学的关键．
练习册系列答案
相关题目
