题目内容
计算题
(1)∫12(
+
+
)dx
(2)
+(
)2000+
.
(1)∫12(
| 1 | ||
|
| 1 |
| x |
| 1 |
| x2 |
(2)
-2
| ||
1+i2
|
| ||
| 1+i |
| 1+i |
| 3-i |
分析:(1)根据积分的运算法则求出函数的原函数,即可求出所求积分的值.
(2)表达式的第一个分式,分子、分母同乘i,第二个求出分式的平方,然后再求1000次方,第三个分式同乘分母的共轭复数化简为a+bi(a,b∈R)的形式即可.
(2)表达式的第一个分式,分子、分母同乘i,第二个求出分式的平方,然后再求1000次方,第三个分式同乘分母的共轭复数化简为a+bi(a,b∈R)的形式即可.
解答:(本小题满分14分)
解:(1)
(
+
+
)dx=(2
+lnx-
)
=2
+ln2-
-2-0+1
=2
-
+ln2
(2)
+(
)2000+
=
+[(
)2]1000+
=
+(
) 1000+
原式的值为:
.
解:(1)
| ∫ | 2 1 |
| 1 | ||
|
| 1 |
| x |
| 1 |
| x2 |
| x |
| 1 |
| x |
| | | 2 1 |
=2
| 2 |
| 1 |
| 2 |
=2
| 2 |
| 3 |
| 2 |
(2)
-2
| ||
1+i2
|
| ||
| 1+i |
| 1+i |
| 3-i |
=
(-2
| ||
(1+i2
|
| ||
| 1+i |
| (1+i)(3+i) |
| (3-i)(3+i) |
=
(-2
| ||
i-2
|
| 2 |
| 2i |
| 2+4i |
| 10 |
|
原式的值为:
|
点评:本题是基础题,(1)考查积分的运算法则;(2)复数代数形式的混合运算,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
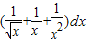
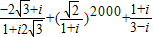 .
.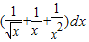
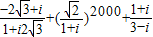 .
.