题目内容
已知函数f(x)=alnx+bx,且f(1)=-1,f′(1)=0,
(1)求f(x);
(2)求f(x)的最大值;
(3)若x>0,y>0,证明:lnx+lny≤ .
.
(1)解:由b=f(1)=-1,f′(1)=a+b=0,∴a=1,
∴f(x)=lnx-x为所求;
(2)解:∵x>0,f′(x)= -1=
-1=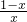 ,当x变化时,f′(x),f(x)变化情况如下表:
,当x变化时,f′(x),f(x)变化情况如下表:
∴f(x)在x=1处取得极大值-1,即所求最大值为-1;
(3)证明:由(2)得lnx≤x-1恒成立,
∴lnx+lny= ≤
≤ +
+ =
= 成立.
成立.
分析:(1)由f(1)=-1,f′(1)=0列方程组解出即可;
(2)求导数f′(x),在定义域内解不等式f′(x)>0,f′(x)<0,以表格形式列出,求出极值点,从而得到最值点,代入即可求得最大值;
(3)由(2)得lnx≤x-1恒成立,lnx+lny= ≤
≤ +
+ ,整理即证;
,整理即证;
点评:本题考查利用导数求函数的最值及证明不等式问题,利用导数证明不等式往往根据前面结论:如最值等.
∴f(x)=lnx-x为所求;
(2)解:∵x>0,f′(x)=
 -1=
-1=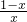 ,当x变化时,f′(x),f(x)变化情况如下表:
,当x变化时,f′(x),f(x)变化情况如下表:| x | 0<x<1 | x=1 | x>1 |
| f′(x) | + | 0 | - |
| f(x) | ↗ | 极大值 | ↘ |
(3)证明:由(2)得lnx≤x-1恒成立,
∴lnx+lny=
 ≤
≤ +
+ =
= 成立.
成立.分析:(1)由f(1)=-1,f′(1)=0列方程组解出即可;
(2)求导数f′(x),在定义域内解不等式f′(x)>0,f′(x)<0,以表格形式列出,求出极值点,从而得到最值点,代入即可求得最大值;
(3)由(2)得lnx≤x-1恒成立,lnx+lny=
 ≤
≤ +
+ ,整理即证;
,整理即证;点评:本题考查利用导数求函数的最值及证明不等式问题,利用导数证明不等式往往根据前面结论:如最值等.

练习册系列答案
相关题目