题目内容
设数列[an]的前N项和为Sn,点(an,Sn)在直线y= x-1上.
x-1上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)在an与a n+1之间插入n个数,使这n+2个数组成公差为dn的等差数列,求数列{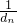 }的前n项和Tn,并求使
}的前n项和Tn,并求使 Tn+
Tn+
 成立的正整数n最小值.
成立的正整数n最小值.
解:(Ⅰ)∵由题设知,
Sn= an-1,①∴a1=S1=
an-1,①∴a1=S1= a1-1,解得a1=2
a1-1,解得a1=2
n≥2时,Sn-1= an-1-1,②
an-1-1,②
①-②可得:an= an-
an- an-1,
an-1,
∴an=3an-1(n≥2),即数列{an}是等比数列
∴an=2•3n-1,
(Ⅱ)由(I)得,an+1=2•3n,an=2•3n-1,
∵an+1=an+(n-1)dn,∴dn=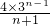 ,
, ,
,
令Tn= +
+ +
+ +
+ +…+
+…+ ,
,
∴ Tn=
Tn= +
+ +
+ +…+
+…+ ,
,
∴ Tn=
Tn= +(
+( +
+ +…+
+…+ )-
)- ,
,
= +
+ ×
× -
- =
= -
- ,
,
∴Tn= -
- .
.
∴
即 ,
,
3n≥81,
得n≥4.
∴使 Tn+
Tn+
 成立的正整数n最小值是4.
成立的正整数n最小值是4.
分析:(Ⅰ)先利用点(an,Sn)在直线y= x-1上得Sn=
x-1上得Sn= an-1,再写一式,两式作差即可求数列{an}的通项;
an-1,再写一式,两式作差即可求数列{an}的通项;
(Ⅱ)先把所求结论代入求出数列{Tn}的通项,再利用数列求和的错位相减法即可求出其各项的和,最后利用不等关系求解即可.
点评:本题考查数列的通项,考查数列求和的错位相减法,考查计算能力,属于中档题.
Sn=
 an-1,①∴a1=S1=
an-1,①∴a1=S1= a1-1,解得a1=2
a1-1,解得a1=2n≥2时,Sn-1=
 an-1-1,②
an-1-1,②①-②可得:an=
 an-
an- an-1,
an-1,∴an=3an-1(n≥2),即数列{an}是等比数列
∴an=2•3n-1,
(Ⅱ)由(I)得,an+1=2•3n,an=2•3n-1,
∵an+1=an+(n-1)dn,∴dn=
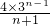 ,
, ,
,令Tn=
 +
+ +
+ +
+ +…+
+…+ ,
,∴
 Tn=
Tn= +
+ +
+ +…+
+…+ ,
,∴
 Tn=
Tn= +(
+( +
+ +…+
+…+ )-
)- ,
,=
 +
+ ×
× -
- =
= -
- ,
,∴Tn=
 -
- .
.∴

即
 ,
,3n≥81,
得n≥4.
∴使
 Tn+
Tn+
 成立的正整数n最小值是4.
成立的正整数n最小值是4.分析:(Ⅰ)先利用点(an,Sn)在直线y=
 x-1上得Sn=
x-1上得Sn= an-1,再写一式,两式作差即可求数列{an}的通项;
an-1,再写一式,两式作差即可求数列{an}的通项;(Ⅱ)先把所求结论代入求出数列{Tn}的通项,再利用数列求和的错位相减法即可求出其各项的和,最后利用不等关系求解即可.
点评:本题考查数列的通项,考查数列求和的错位相减法,考查计算能力,属于中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目