题目内容
已知函数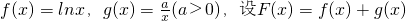 .
.
(I)求函数F(x)的单调区间;
(II)若以函数y=F(x)(x∈(0,3])的图象上任意一点P(x0,y0)为切点的切线的斜率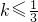 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;
(III)是否存在实数m,使得函数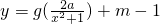 的图象与函数y=f(1+x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
的图象与函数y=f(1+x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
解:(I)∵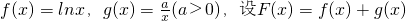 .
.
∴F'(x)= -
- =
=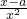 ,(x>0);
,(x>0);
∵x>0;
所以:F'(x)>0?x>a.
∴F(x)在(a,+∞)上递增;
F'(x)<0?0<x<a,
F(x)在(0,a)上递减.
所以:函数F(x)的单调增区间为(a,+∞),单调减区间为(0,a).
(II)因为:F'(x)=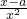 (0<x≤3),
(0<x≤3),
则k=F'(x0)= ≤
≤ 恒成立;
恒成立;
即a≥-
 +x0在(0,3]上恒成立,
+x0在(0,3]上恒成立,
当x0= 时,-
时,-
 +x0取最大值
+x0取最大值 ,
,
∴a≥ .
.
即a的最小值为 .
.
(III)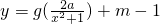 =
= x2+m-
x2+m- 的图象与函数y=f(1+x2)=ln(1+x2)的图象恰有四个不同的交点,
的图象与函数y=f(1+x2)=ln(1+x2)的图象恰有四个不同的交点,
即, x2+m-
x2+m- =ln(1+x2)有四个不同的根,亦即m=ln(1+x2)-
=ln(1+x2)有四个不同的根,亦即m=ln(1+x2)- x2-
x2- 有四个不同的根;
有四个不同的根;
令G(x)=ln(1+x2)- x2-
x2- ;
;
则G'(x)=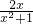 -x=
-x= =
= ;
;
当x变化时,G'(x),G(x)的变化情况如下表,
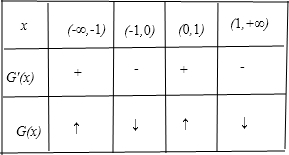
由表格知,G(x)的极小值G(0)= ,G(x)的极大值G(1)=G(-1)=ln2>0.
,G(x)的极大值G(1)=G(-1)=ln2>0.
∴m∈( ,ln2),y=G(x)与y=m恰有四个不同的交点,
,ln2),y=G(x)与y=m恰有四个不同的交点,
即当m∈( ,ln2)时,函数
,ln2)时,函数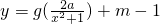 的图象与函数y=f(1+x2)的图象恰有四个不同的交点.
的图象与函数y=f(1+x2)的图象恰有四个不同的交点.
分析:(I)先求出其导函数,根据导函数的正负即可求出其单调区间;
(II)先把问题转化为F'(x0)= ≤
≤ 恒成立;再结合二次函数即可求出结论;
恒成立;再结合二次函数即可求出结论;
(III)先根据条件把问题转化为m=ln(1+x2)- x2-
x2- 有四个不同的根;求出其导函数,找到其极值点,根据极值即可得到结论.
有四个不同的根;求出其导函数,找到其极值点,根据极值即可得到结论.
点评:本题主要考察了应用导数求函数的单调区间,极值,最值,以及恒成立问题的判断.
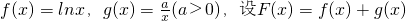 .
.∴F'(x)=
 -
- =
=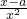 ,(x>0);
,(x>0);∵x>0;
所以:F'(x)>0?x>a.
∴F(x)在(a,+∞)上递增;
F'(x)<0?0<x<a,
F(x)在(0,a)上递减.
所以:函数F(x)的单调增区间为(a,+∞),单调减区间为(0,a).
(II)因为:F'(x)=
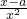 (0<x≤3),
(0<x≤3),则k=F'(x0)=
 ≤
≤ 恒成立;
恒成立;即a≥-

 +x0在(0,3]上恒成立,
+x0在(0,3]上恒成立,当x0=
 时,-
时,-
 +x0取最大值
+x0取最大值 ,
,∴a≥
 .
.即a的最小值为
 .
.(III)
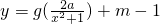 =
= x2+m-
x2+m- 的图象与函数y=f(1+x2)=ln(1+x2)的图象恰有四个不同的交点,
的图象与函数y=f(1+x2)=ln(1+x2)的图象恰有四个不同的交点,即,
 x2+m-
x2+m- =ln(1+x2)有四个不同的根,亦即m=ln(1+x2)-
=ln(1+x2)有四个不同的根,亦即m=ln(1+x2)- x2-
x2- 有四个不同的根;
有四个不同的根;令G(x)=ln(1+x2)-
 x2-
x2- ;
;则G'(x)=
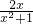 -x=
-x= =
= ;
;当x变化时,G'(x),G(x)的变化情况如下表,

由表格知,G(x)的极小值G(0)=
 ,G(x)的极大值G(1)=G(-1)=ln2>0.
,G(x)的极大值G(1)=G(-1)=ln2>0.∴m∈(
 ,ln2),y=G(x)与y=m恰有四个不同的交点,
,ln2),y=G(x)与y=m恰有四个不同的交点,即当m∈(
 ,ln2)时,函数
,ln2)时,函数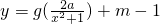 的图象与函数y=f(1+x2)的图象恰有四个不同的交点.
的图象与函数y=f(1+x2)的图象恰有四个不同的交点.分析:(I)先求出其导函数,根据导函数的正负即可求出其单调区间;
(II)先把问题转化为F'(x0)=
 ≤
≤ 恒成立;再结合二次函数即可求出结论;
恒成立;再结合二次函数即可求出结论;(III)先根据条件把问题转化为m=ln(1+x2)-
 x2-
x2- 有四个不同的根;求出其导函数,找到其极值点,根据极值即可得到结论.
有四个不同的根;求出其导函数,找到其极值点,根据极值即可得到结论.点评:本题主要考察了应用导数求函数的单调区间,极值,最值,以及恒成立问题的判断.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.