题目内容
已知圆锥曲线C上任意一点到两定点F1(-1,0)、F2(1,0)的距离之和为常数,曲线C的离心率e=
.
(1)求圆锥曲线C的方程;
(2)设经过点F2的任意一条直线与圆锥曲线C相交于A、B,试证明在x轴上存在一个定点P,使
•
的值是常数.
| 1 |
| 2 |
(1)求圆锥曲线C的方程;
(2)设经过点F2的任意一条直线与圆锥曲线C相交于A、B,试证明在x轴上存在一个定点P,使
| PA |
| PB |
(1)依题意,设曲线C的方程为
+
=1(a>b>0),
∴c=1,
∵e=
=
,
∴a=2,
∴b=
=
,
所求方程为
+
=1.
(2)当直线AB不与x轴垂直时,设其方程为y=k(x-1),
由
,
得(3+4k2)x2-8k2x+4(k2-3)=0,
从而xA+xB=
,xA•xB=
,
设P(t,0),则
•
=(xA-t)(xB-t)+yAyB=(k2+1)xAxB-(t+k2)(xA+xB)+(k2+t2)=
当
=
,
解得t=
此时对?k∈R,
•
=-
;
当AB⊥x轴时,直线AB的方程为x=1,
xA=xB=1,yA(yB)=±
,
对t=
,
•
=(xA-t)(xB-t)+yAyB=
-
=-
,
即存在x轴上的点P(
,0),使
•
的值为常数-
.
| x2 |
| a2 |
| y2 |
| b2 |
∴c=1,
∵e=
| c |
| a |
| 1 |
| 2 |
∴a=2,
∴b=
| a2-c2 |
| 3 |
所求方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)当直线AB不与x轴垂直时,设其方程为y=k(x-1),
由
|
得(3+4k2)x2-8k2x+4(k2-3)=0,
从而xA+xB=
| 8k2 |
| 3+4k2 |
| 4(k2-3) |
| 3+4k2 |
设P(t,0),则
| PA |
| PB |
| 3t2-12+(-5-8t+4t2)k2 |
| 3+4k2 |
当
| 3t2-12 |
| 3 |
| -5-8t+4t2 |
| 4 |
解得t=
| 11 |
| 8 |
此时对?k∈R,
| PA |
| PB |
| 135 |
| 64 |
当AB⊥x轴时,直线AB的方程为x=1,
xA=xB=1,yA(yB)=±
| 3 |
| 2 |
对t=
| 11 |
| 8 |
| PA |
| PB |
| 9 |
| 64 |
| 9 |
| 4 |
| 135 |
| 64 |
即存在x轴上的点P(
| 11 |
| 8 |
| PA |
| PB |
| 135 |
| 64 |

练习册系列答案
相关题目
 .
. 的值是常数.
的值是常数.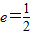 .
.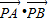 的值是常数.
的值是常数.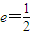 .
.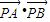 的值是常数.
的值是常数.