题目内容
设集合A={x|log2x<1},B={x|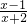 <0},则A∩B=________.
<0},则A∩B=________.
{x|0<x<1}
分析:把集合A中的1变为log22,然后利用对数函数的定义域和对数函数为增函数即可求出x的范围即可得到集合A;由集合B中的不等式得到x-1与x+2异号,列出不等式求出解集即可得到集合B,然后求出A与B的交集即可.
解答:由已知,集合A中的不等式log2x<1=log22,由2>1得到对数函数为增函数及对数函数的定义域为:x>0得到:0<x<2;而集合B中的不等式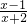 <0可化为
<0可化为 或
或 ,解得-2<x<1,
,解得-2<x<1,
则A={x|0<x<2},B={x|-2<x<1},所以A∩B={x|0<x<1}
故答案为:{x|0<x<1}
点评:本题考查学生会求对数函数的定义域以及灵活运用对数函数的增减性解决实际问题,理解不等式 <0
<0
与不等式(x-a)(x-b)<0同解,掌握交集的定义并会进行交集的运算.
分析:把集合A中的1变为log22,然后利用对数函数的定义域和对数函数为增函数即可求出x的范围即可得到集合A;由集合B中的不等式得到x-1与x+2异号,列出不等式求出解集即可得到集合B,然后求出A与B的交集即可.
解答:由已知,集合A中的不等式log2x<1=log22,由2>1得到对数函数为增函数及对数函数的定义域为:x>0得到:0<x<2;而集合B中的不等式
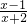 <0可化为
<0可化为 或
或 ,解得-2<x<1,
,解得-2<x<1,则A={x|0<x<2},B={x|-2<x<1},所以A∩B={x|0<x<1}
故答案为:{x|0<x<1}
点评:本题考查学生会求对数函数的定义域以及灵活运用对数函数的增减性解决实际问题,理解不等式
 <0
<0与不等式(x-a)(x-b)<0同解,掌握交集的定义并会进行交集的运算.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目