题目内容
已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为实数,
为实数,![]() 为正整数.
为正整数.
(Ⅰ)证明:对任意实数![]() ,数列
,数列![]() 不是等比数列;
不是等比数列;
(Ⅱ)证明:当![]() 时,数列
时,数列![]() 是等比数列;
是等比数列;
(Ⅲ)设![]() 为数列
为数列![]() 的前n项和,是否存在实数
的前n项和,是否存在实数![]() ,使得对任意正整数n,都有
,使得对任意正整数n,都有
![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(Ⅰ)证明:假设存在一个实数,使{an}是等比数列,则有![]() ,即
,即
![]() 矛盾.
矛盾.
所以{an}不是等比数列.
(Ⅱ)证明:![]()
![]()
![]()
![]() 又
又![]() ,
,![]() ,由上式知
,由上式知![]() ,
,![]()
![]() 故当
故当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(Ⅲ)当![]() 时,由(Ⅱ)得
时,由(Ⅱ)得![]() ,于是
,于是

当![]() 时,
时,![]() ,从而
,从而![]() 上式仍成立.
上式仍成立.
要使对任意正整数n , 都有![]() ,
,
即 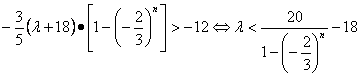
令![]() ,则
,则
当n为正奇数时,![]() 当n为正偶数时,
当n为正偶数时,![]()
![]()
于是可得![]()
综上所述,存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]()
![]()
![]() 的取值范围为
的取值范围为![]() 。
。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 和
和 满足:
满足: ,
, 其中
其中 为实数,
为实数, 为正整数.
为正整数. ;
; ,是否存在实数
,是否存在实数 成立? 若存在,求
成立? 若存在,求 和
和 满足:
满足: ,其中
,其中 为实数,n为正整数,数列
为实数,n为正整数,数列
 ,并求
,并求
 ,试求数列
,试求数列 的最大项和最小项;
的最大项和最小项; ,是否存在实数
,是否存在实数 成立?若存在,求
成立?若存在,求 和
和 满足
满足 
 时,求证:对于任意的实数
时,求证:对于任意的实数 ,
, 一定不是等差数列;
一定不是等差数列; 时,试判断
时,试判断 是否为等比数列;
是否为等比数列;