题目内容
定义域为R的函数f(x)=
若方程f2(x)+bf(x)+c=0有且只有3个不同的实数根x1、x2、x3，则x1+x2+x3=________________.
3
解析：本题考查函数方程思想、数形结合思想以及分析问题解决问题的能力，在方法能力方面要求较高.
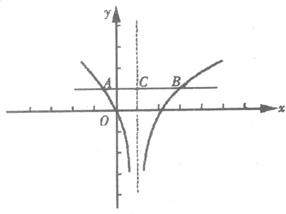
作出函数f(x)的图像，如图：方程f2(x)+bf(x)+c=0是关于f(x)的二次方程，设其两根为f(x1)，f(x2)即f2(x)+bf(x)+c=[f(x)-f(x1)][f(x)-f(x2)]，当f(x1)，f(x2)≠1时，f(x)-f(x1)=0以及f(x)-f(x1)=0都有2个实根，故不可能出现3个实根，当原方程有3个实根时，当且仅当f(x1)=f(x2)=1，即f2(x)+bf(x)+c=[f(x)-1]2=0，此时x1+x2+x3=3x2=3.
练习册系列答案
相关题目