题目内容

定义一种运算如下：
x1y1
x2y2
=x1y2-x2y1，复数z=
3
+i		-1
3
-i		i
（i是虚数单位）的共轭复数是（　　）
A、
3
-1+(
3
-1)i
B、
3
-1-(
3
-1)i
C、
3
+1+(
3
+1)i
D、
3
+1-(
3
+1)i
分析：根据条件中定义的行列式，写出含有复数的行列式的结果，根据共轭复数的定义，直接写出共轭复数即可．
解答：解：
∵行列式的运算定义为
.
x1y1
x2y2
.
=x1y2-x2y1，
∴z=
.
3
+i		-1
3
-i		i
.
=
3
i-1+
3
 -i=（
3
-1）+（
3
-1）i，
所以它的共轭复数为：
3
-1-(
3
-1)i．
故选B．
点评：本题是一个新定义问题，考查同学们的理解能力，解题的关键是理解行列式的展开式．
练习册系列答案
相关题目
在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
（1）对任意a，b∈R，a*b=b*a；
（2）对任意a∈R，a*0=a；
（3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
关于函数f(x)=(2x)*
1
2x
的性质，有如下说法：
①函数f（x）的最小值为3；
②函数f（x）为奇函数；
③函数f（x）的单调递增区间为(-∞，-
1
2
)，(
1
2
，+∞)．
其中所有正确说法的个数为（　　）
A、0B、1C、2D、3
定义平面向量之间的一种运算“⊙”如下：对任意的向量a=（m，n），b=（p，q），令a⊙b=（m+p，n-q），已知a=（cosθ，3），b=(sinθ，3+
2
sinθ)（θ∈R），点N（x，y）满足
ON
=a⊙b（其中O为坐标原点），则|
ON
|2的最大值为（　　）
A、
2
B、2+
2
C、2-
2
D、2
在实数集R中定义一种运算“*”，对于任意给定的a，b∈R，a*b为唯一确定的实数，且具有性质；
（1）对任意a，b∈R，a*b=b*a；
（2）对任意a∈R，a*0=a；
（3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
关于函数f(x)=(3x)*(
1
3x
)的性质，有如下说法：
①函数f（x）的最小值为3；
②函数f（x）为奇函数；
③函数f（x）的单调递增区间为(-∞，-
1
3
)，(
1
3
，+∞)．
其中所有正确说法的序号为
③
③
．
在实数集R中定义一种运算“*”，对于任意给定的a，b∈R，a*b为唯一确定的实数，且具有性质；
（1）对任意a，b∈R，a*b=b*a；
（2）对任意a∈R，a*0=a；
（3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
关于函数的性质，有如下说法：
①函数f（x）的最小值为3；
②函数f（x）为奇函数；
③函数f（x）的单调递增区间为．
其中所有正确说法的序号为    ．
定义平面向量之间的一种运算“⊙”如下：对任意的向量a=（m，n），b=（p，q），令a⊙b=（m+p，n-q），已知a=（cosθ，3），b=（θ∈R），点N（x，y）满足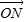=a⊙b（其中O为坐标原点），则的最大值为（ ）
A．
B．
C．
D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网