题目内容
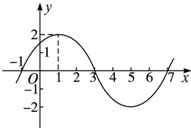 (2013•东城区模拟)已知函数f(x)=Asin(ω+φ)(A>0,ω>0,|φ|<
(2013•东城区模拟)已知函数f(x)=Asin(ω+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数y=f(x)+2cos(
| π |
| 4 |
| π |
| 4 |
| 2 |
| 3 |
分析:(Ⅰ)直接利用函数的图象求出A,以及函数的周期,求出ω,利用f(1)=2,结合φ的范围求出φ的值,即可求函数f(x)的解析式;
(Ⅱ)化简函数y=f(x)+2cos(
x+
)的表达式,通过x∈[-6,-
],求出相位的范围,利用余弦函数的值域求出函数的最大值和最小值.
(Ⅱ)化简函数y=f(x)+2cos(
| π |
| 4 |
| π |
| 4 |
| 2 |
| 3 |
解答:(共13分)
解:(Ⅰ)由图可知:A=2,-------------------------------(1分)
最小正周期T=
=8,所以ω=
.----------------------(2分)
f(1)=2,即sin(
+φ)=1,又|φ|<
,所以φ=
.--------(5分)
所以f(x)=2sin(
x+
).---------------------------------(6分)
(Ⅱ)函数y=f(x)+2cos(
x+
)=2sin(
x+
)+2cos(
x+
)=2
cos
x.------------(9分)
由x∈[-6,-
]得
x∈[-
,-
],-----------------------(11分)
所以,当
x=-π,即x=-4时,y取最小值-2
;--------(12分)
当
x=-
,即x=-
时,y取最大值
.----------------(13分)
解:(Ⅰ)由图可知:A=2,-------------------------------(1分)
最小正周期T=
| 2π |
| ω |
| π |
| 4 |
f(1)=2,即sin(
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
所以f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
(Ⅱ)函数y=f(x)+2cos(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
由x∈[-6,-
| 2 |
| 3 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 6 |
所以,当
| π |
| 4 |
| 2 |
当
| π |
| 4 |
| π |
| 6 |
| 2 |
| 3 |
| 6 |
点评:本题考查三角函数的解析式的求法,函数的值域的应用,考查三角函数的图象与性质.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 (2013•东城区二模)如图,△BCD是等边三角形,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.
(2013•东城区二模)如图,△BCD是等边三角形,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.