题目内容
13.函数y=x4(2-x2)(0<x<$\sqrt{2}$)的最大值是( )| A. | 0 | B. | 1 | C. | $\frac{16}{27}$ | D. | $\frac{32}{27}$ |
分析 利用导数求得函数的单调性,继而求得最大值.
解答 解:y'=8x3-6x5(0<x<$\sqrt{2}$)
令y'=0
解得x=0,或x=$\frac{2\sqrt{3}}{3}$或x=-$\frac{2\sqrt{3}}{3}$
因为0<x<$\sqrt{2}$,令y'>0,解得$0<x<\frac{2\sqrt{3}}{3}$,即函数在($0,\frac{2\sqrt{3}}{3}$)上单调递增
同样求得函数在($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$)上单调递减.
所以ymax=$(\frac{2\sqrt{3}}{3})^{4}(2-(\frac{2\sqrt{3}}{3})^{2})=\frac{16}{9}×\frac{2}{3}=\frac{32}{27}$
故选D
点评 本题主要考查了利用导数求得函数在某一区间段上的最值问题,属于简单题型.

练习册系列答案
相关题目
8.已知角θ的终边经过点P(4,m),且sinθ=$\frac{3}{5}$,则m等于( )
| A. | -3 | B. | 3 | C. | $\frac{16}{3}$ | D. | ±3 |
18.在△ABC中,E为AC上一点,且$\overrightarrow{AC}=4\overrightarrow{AE}$,P为BE上一点,且$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),则$\frac{1}{m}+\frac{1}{n}$取最小值时,向量$\overrightarrow{a}$=(m,n)的模为( )
| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{5}}}{6}$ | D. | 2 |
5.将函数y=sin2x的图象向左平移φ(0<φ<π)个单位后得函数$y=sin({2x-\frac{π}{3}})$的图象,则φ的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
2.某校通过随机询问100名性别不同的学生是否能做到“光盘”行动,得到所示联表:
附:K2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$,则下列结论正确的是( )
| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k) | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过1%的前提下,认为“该校学生能否做到‘光盘’与性别无关” | |
| B. | 有99%以上的把握认为“该校学生能否做到‘光盘’与性别有关” | |
| C. | 在犯错误的概率不超过10%的前提下,认为“该校学生能否做到‘光盘’与性别有关” | |
| D. | 有90%以上的把握认为“该校学生能否做到‘光盘’与性别无关” |
3.已知实数x,y满足$\left\{\begin{array}{l}x+y≥1\\{x^2}+{y^2}≤1\end{array}\right.$,则2x+y的取值范围是( )
| A. | [1,2] | B. | [1,+∞) | C. | $(0,\sqrt{5}]$ | D. | $[1,\sqrt{5}]$ |
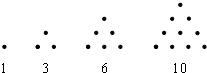 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数:
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数: