题目内容
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
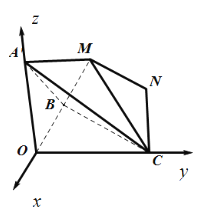
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
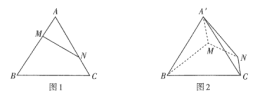
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() .在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段
.在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
【答案】(1)见解析(2)见解析
【解析】
(1)要证明平面![]() 平面
平面![]() ,只需证明
,只需证明![]() 平面
平面![]() 即可;
即可;
(2)选择条件①②③之一,均需建系,算得向量![]() 以及平面
以及平面![]() 的法向量,设直线
的法向量,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,利用
,利用![]() 计算即可.
计算即可.
(1)由已知得![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
解得![]() ,故
,故![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,又∵
,又∵![]() ,
,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)(ⅰ)若用条件①![]() ,由(1)得
,由(1)得![]() ,
,![]() 和
和![]() 是两条相交直线,∴
是两条相交直线,∴![]() 平面
平面![]() .
.
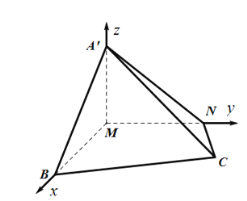
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,设
,设![]() ,其中
,其中![]() ,则
,则![]() .
.
平面![]() 的法向量为
的法向量为![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则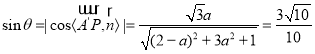 ,解得
,解得![]() ,
,
所以不存在![]() 满足条件.
满足条件.
(ⅱ)若用条件②二面角![]() 大小为
大小为![]() ,由(1)得
,由(1)得![]() 是二面角
是二面角![]() 的平面角,
的平面角,
∴![]() .过
.过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 平面
平面![]() .
.
在平面![]() 中,作
中,作![]() ,点
,点![]() 在
在![]() 的右侧.
的右侧.
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则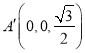 ,设
,设![]() ,其中
,其中![]() ,则
,则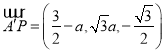 .
.
平面![]() 的法向量为
的法向量为![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则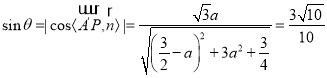 ,
,
解得![]() 或
或![]() (舍去),所以存在
(舍去),所以存在![]() 满足条件,这时
满足条件,这时![]() .
.
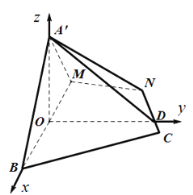
(ⅲ)若用条件③![]() ,在
,在![]() 中,由余弦定理得:
中,由余弦定理得:
![]() ,即
,即![]() ,
,
所以![]() ,故
,故![]() .
.
过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 平面
平面![]() .
.
同(ⅱ)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则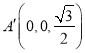 ,设
,设![]() ,其中
,其中![]() ,则
,则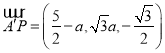 .
.
平面![]() 的法向量为
的法向量为![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则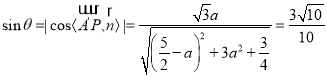 ,
,![]() .
.
解得![]() ,所以不存在
,所以不存在![]() 满足条件.
满足条件.
【点晴】
本题考查面面垂直的判定定理,以及利用向量法求线面角的问题,考查学生数学运算能力,空间想象能力,是一道中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目