题目内容
将一颗骰子掷两次，观察出现的点数，并记第一次出现的点数为m，第二次出现的点数为n，向量
=（m，n），
=（3，6），则向量
与
共线的概率为______．
| p |
| q |
| p |
| q |
由题意知本题是一个古典概型，
∵试验发生包含的事件是一颗骰子掷两次，共有6×6=36种结果，
满足条件事件是向量
=（m，n）与
=（3，6）共线，
即6m-3n=0，
∴n=2m，
满足这种条件的有（1，2）（2，4）（3，6），共有3种结果，
∴向量
与
共线的概率P=
=
，
故答案为：
∵试验发生包含的事件是一颗骰子掷两次，共有6×6=36种结果，
满足条件事件是向量
| p |
| q |
即6m-3n=0，
∴n=2m，
满足这种条件的有（1，2）（2，4）（3，6），共有3种结果，
∴向量
| p |
| q |
| 3 |
| 36 |
| 1 |
| 12 |
故答案为：
| 1 |
| 12 |
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
=(m,n),
= (3,6)，则向量
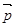=(m,n),
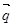=(3,6),则向量