题目内容
在△ABC中,三个内角是A,B,C的对边分别是a,b,c,其中c=10,且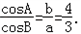
(1)求证:△ABC是直角三角形;
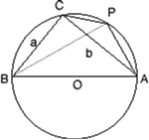
(2)设圆O过A,B,C三点,点P位于劣弧AC上,∠PAB=60°,求四边形ABCP的面积.
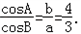
(1)求证:△ABC是直角三角形;
(2)设圆O过A,B,C三点,点P位于劣弧AC上,∠PAB=60°,求四边形ABCP的面积.
解:(1)证明:根据正弦定理得,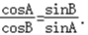
整理为:sinAcosA=sinBcosB,即2sinA=sin2B,
因为0<A<π,0<B<π,
所以0<2A<2π,0<2B<2π,
所以A=B,或者A+B=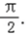
由于 ,
,
故△ABC是直角三角形.
(2)由(1)可得:a=6,b=8.
在Rt△ABC中,sin∠CAB=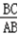 =
= 
cos∠CAB= sin∠PAC=sin(60°﹣∠CAB)
sin∠PAC=sin(60°﹣∠CAB)
=sin60°cos∠CAB﹣cos60°sin∠CAB =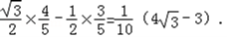
连接PB,在Rt△APB中,AP=AB×cos∠PAB=5.
所以四边形ABCP的面积
S四边形△ABCP=S△ABC+S△PAC
=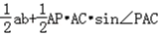
=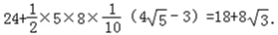
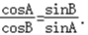
整理为:sinAcosA=sinBcosB,即2sinA=sin2B,
因为0<A<π,0<B<π,
所以0<2A<2π,0<2B<2π,
所以A=B,或者A+B=
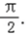
由于
 ,
,故△ABC是直角三角形.
(2)由(1)可得:a=6,b=8.
在Rt△ABC中,sin∠CAB=
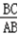 =
= 
cos∠CAB=
 sin∠PAC=sin(60°﹣∠CAB)
sin∠PAC=sin(60°﹣∠CAB) =sin60°cos∠CAB﹣cos60°sin∠CAB =
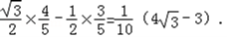
连接PB,在Rt△APB中,AP=AB×cos∠PAB=5.
所以四边形ABCP的面积
S四边形△ABCP=S△ABC+S△PAC
=
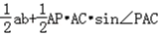
=
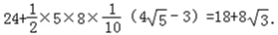


练习册系列答案
相关题目