Question

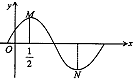（2012•厦门模拟）函数y=sin（ωx+φ）在一个周期内的图象如图所示，M、N分别是最高、最低点，O为坐标原点且

OM

•

ON

=0，则函数f（x）的最小正周期为（　　）

• A．

  3

  2

• B．

  5

  2

• C．3
• D．4

Answer 1

分析：设函数的周期为T，结合函数图象可得点M、N的坐标，从而得到向量

OM

、

ON

的坐标，利用数量积的坐标运算公式，建立关于T的方程并解之，可得周期T的值．

解答：解：设函数的周期为T
∵函数y=sin（ωx+φ）的最大值为1，最小值为-1
∴M的坐标为（

1

2

，1），N的坐标为（

1

2

+

T

2

，-1）
可得

OM

=（

1

2

，1），

ON

=（

1

2

+

T

2

，-1）
∴

OM

•

ON

=

1

2

（

1

2

+

T

2

）+1×（-1）=0，解之得T=3
故选C

点评：本题给出三角函数图象上两个最值点M、N在已知

OM

•

ON

=0的情况下求函数的周期，着重考查了向量的数量积和三角函数的图象与性质等知识，属于基础题．