题目内容
设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)写出一个正整数![]() ,使得
,使得![]() 是数列
是数列![]() 的项;
的项;
(3)设数列![]() 的通项公式为
的通项公式为![]() ,问:是否存在正整数
,问:是否存在正整数![]() 和
和![]() (
(![]() ),使得
),使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,请求出所有符合条件的有序整数对
成等差数列?若存在,请求出所有符合条件的有序整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)设数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,由已知,有
,由已知,有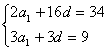
解得![]() ,
,![]() ,
,
所以![]() 的通项公式为
的通项公式为![]() (
(![]() ).
).
(2)当![]() 时,
时,![]() ,所以
,所以![]()
由![]() ,得
,得![]() ,两式相减,得
,两式相减,得![]() ,
,
故![]() ,……(2分)
,……(2分)
所以,![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,所以
的等比数列,所以![]() .
.
![]() ,
,
要使![]() 是
是![]() 中的项,只要
中的项,只要![]() 即可,可取
即可,可取![]() .
.
(只要写出一个![]() 的值就给分,写出
的值就给分,写出![]() ,
,![]() ,
,![]() 也给分)
也给分)
(3)由(1)知,![]() ,
,
要使![]() ,
,![]() ,
,![]() 成等差数列,必须
成等差数列,必须![]() ,即
,即
![]() ,
,
化简得![]() .
.
因为![]() 与
与![]() 都是正整数,所以
都是正整数,所以![]() 只能取
只能取![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
综上可知,存在符合条件的正整数![]() 和
和![]() ,所有符合条件的有序整数对
,所有符合条件的有序整数对![]() 为:
为:
![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 且满足
且满足 则
则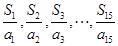 中最大的项为( )
中最大的项为( ) B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,已知
,已知 ,
, ,则
,则 .
.