题目内容
已知函数f(x)的图象与函数h(x)=x+ +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)(文)若g(x)=f(x)•x+ax,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
(理)若g(x)=f(x)+ ,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
解:(1)设f(x)图象上任一点坐标为(x,y),点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)的图象上.
∴2-y=-x+ +2.
+2.
∴y=x+ ,即f(x)=x+
,即f(x)=x+ .
.
(2)(文)g(x)=(x+ )•x+ax,
)•x+ax,
即g(x)=x2+ax+1.
g(x)在(0,2]上递减?- ≥2,
≥2,
∴a≤-4.
(理)g(x)=x+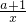 .
.
∵g′(x)=1-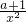 ,g(x)在(0,2]上递减,
,g(x)在(0,2]上递减,
∴1-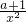 ≤0在x∈(0,2]时恒成立,
≤0在x∈(0,2]时恒成立,
即a≥x2-1在x∈(0,2]时恒成立.
∵x∈(0,2]时,(x2-1)max=3,
∴a≥3.
分析:(1)设f(x)图象上任一点坐标为(x,y),点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)的图象上.由此可求出f(x).
(2)(文)由题意知g(x)=x2+ax+1.由g(x)在(0,2]上递减可得到实数a的取值范围.
(理)由题意知g′(x)=1-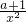 ,g(x)在(0,2]上递减,1-
,g(x)在(0,2]上递减,1-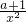 ≤0在x∈(0,2]时恒成立,由此能够推导出a的范围.
≤0在x∈(0,2]时恒成立,由此能够推导出a的范围.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.
∴2-y=-x+
 +2.
+2.∴y=x+
 ,即f(x)=x+
,即f(x)=x+ .
.(2)(文)g(x)=(x+
 )•x+ax,
)•x+ax,即g(x)=x2+ax+1.
g(x)在(0,2]上递减?-
 ≥2,
≥2,∴a≤-4.
(理)g(x)=x+
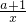 .
.∵g′(x)=1-
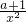 ,g(x)在(0,2]上递减,
,g(x)在(0,2]上递减,∴1-
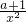 ≤0在x∈(0,2]时恒成立,
≤0在x∈(0,2]时恒成立,即a≥x2-1在x∈(0,2]时恒成立.
∵x∈(0,2]时,(x2-1)max=3,
∴a≥3.
分析:(1)设f(x)图象上任一点坐标为(x,y),点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)的图象上.由此可求出f(x).
(2)(文)由题意知g(x)=x2+ax+1.由g(x)在(0,2]上递减可得到实数a的取值范围.
(理)由题意知g′(x)=1-
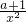 ,g(x)在(0,2]上递减,1-
,g(x)在(0,2]上递减,1-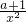 ≤0在x∈(0,2]时恒成立,由此能够推导出a的范围.
≤0在x∈(0,2]时恒成立,由此能够推导出a的范围.点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(