题目内容
正三棱柱ABC—A1B1C1的所有棱长都为2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H.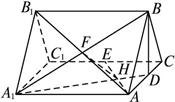
(1)求证:AE⊥平面A1BD;
(2)求二面角DBA1A的大小(用反三角函数表示结果);
(3)求点B1到平面A1BD的距离.
(1)证明:∵ACC1A1是正方形,D是棱AC的中点,E是棱CC1的中点,
∴tan∠EAC=tan∠DA1A=![]() .
.
∴∠EAC=∠DA1A.
∵∠ADA1+∠DA1A=90°,
∴∠ADA1+∠EAC=90°.∴AE⊥A1D.
∵BA=BC,D是棱AC的中点,∴BD⊥AC.
∵平面ABC⊥平面ACC1A1,
∴BD⊥平面ACC1A1.
∴AE⊥BD.
∴AE⊥平面A1BD.
(2)解:连结AB1,交A1B于F,连结HF.

∵ABB1A1是正方形,∴AB1⊥A1B.
∵AE⊥平面A1BD,∴HF⊥A1B.
∴∠AFH是二面角D-BA1-A的平面角.
在正方形ABB1A1中,AF=![]() .
.
在Rt△ADA1中,AH=![]() =
=![]() .
.
在Rt△AFH中,sin∠AFH=![]() =
=![]() ,
,
即二面角DBA1A的大小是arcsin![]() .
.
(3)解:设点B1到平面A1BD的距离为h,则三棱锥B1—A1BD的体积![]() =
=![]() h
h![]() .
.
又∵![]() =
=![]() =
=![]() =
=![]() AH·
AH·![]() ,
,
∴点B1到平面A1BD的距离h=AH=![]() .
.

 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.