题目内容
已知x是奇函数，当x＜0时f（x）=x（x+2），则当x＞0时，f（x）= ．
【答案】分析：设x＞0，则-x＜0，适合已知中的解析式，再由奇函数的性质可得答案．
解答：解：设x＞0，则-x＜0
∴f（-x）=-x（-x+2）=x2-2x
又∵f（x）是奇函数
∴f（x）=-f（-x）=-x2+2x，
故答案为：-x2+2x
点评：本题主要考查用奇偶性求对称区间上的解析式，利用好函数的性质是解决问题的关键，属基础题．
解答：解：设x＞0，则-x＜0
∴f（-x）=-x（-x+2）=x2-2x
又∵f（x）是奇函数
∴f（x）=-f（-x）=-x2+2x，
故答案为：-x2+2x
点评：本题主要考查用奇偶性求对称区间上的解析式，利用好函数的性质是解决问题的关键，属基础题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
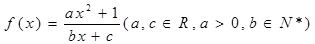是奇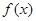
有最小值2，且f （1）
．
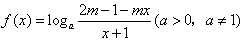是奇函数，定义域为区间D（使表达式有意义的实数x 的集合），
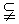D，a是底数）时，函数值组成的集合为[1，+∞)，求实数a、b的值。