Question

【题目】已知

（1）求函数在区间上的最小值；

（2）对一切实数恒成立，求实数的取值范围；

（3）证明：对一切， 恒成立.

Answer 1

【答案】（1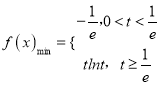）;（2）4；（3）见解析.

【解析】试题分析：（1）求出，分三种情况讨论，分别令 得增区间， 得减区间，从而可得函数在区间上的最小值；（2）等价于，只需以即可；（3）问题等价于证明，由的最小值是， 最大值为.

试题解析：（1），当， ， 单调递减，当， ，

单调递增．············ 2分

①，t无解；

②，即时，

③，即时， 在上单调递增，

所以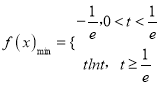．········· 5分

（2），则，

设，则，

， ， 单调递增， ， ，

单调递减，所以，因为对一切， 恒成立，

所以；

（3）问题等价于证明，

由⑴可知的最小值是，当且仅当时取到，

设，则，易得，当且仅当时取到，从而对一切，都有成立．