题目内容
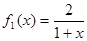 ,定义
,定义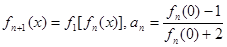 ,其中n∈N*.
,其中n∈N*.(Ⅰ)求
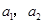 的值,并求证:数列{an}是等比数列;
的值,并求证:数列{an}是等比数列;(II)若
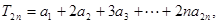
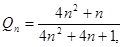 ,其中n∈N*,试比较9
,其中n∈N*,试比较9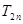 与
与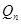 大小,并说明理由.
大小,并说明理由.(1) ,
,
数列{an}是首项为 ,公比为
,公比为 的等比数列。 (2)9
的等比数列。 (2)9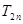 >
>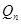 .
.
 ,
,
数列{an}是首项为
 ,公比为
,公比为 的等比数列。 (2)9
的等比数列。 (2)9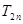 >
>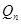 .
.本试题主要是考查了数列的求和和数列的通项公式的 运用。证明数列是否为等比数列以及关于数列的单调性的运用。比较大小。
(1)对n赋值得到前两项,然后发现规律得到
 ,从而证明等比数列
,从而证明等比数列
(2)由(1)知 ,然后利用分组求和得到前n项和的结论,并利用作差法比较大小。
,然后利用分组求和得到前n项和的结论,并利用作差法比较大小。
证明:(1) =2,
=2, ,
,

 ,
,
∴
∴ ,∴数列{an}是首项为
,∴数列{an}是首项为 ,公比为
,公比为 的等比数列。
的等比数列。
(2)由(1)知
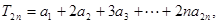

两式相减得:
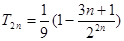
 ,又
,又
当n=1时,9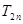 <
<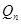 ;
;
当n=2时,9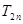 <
<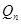 ;
;
当n≥3时,22n=[(1+1)n]2=( )2>(2n+1)2,∴9
)2>(2n+1)2,∴9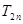 >
>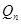 .
.
(1)对n赋值得到前两项,然后发现规律得到
 ,从而证明等比数列
,从而证明等比数列(2)由(1)知
 ,然后利用分组求和得到前n项和的结论,并利用作差法比较大小。
,然后利用分组求和得到前n项和的结论,并利用作差法比较大小。证明:(1)
 =2,
=2, ,
, 
 ,
,∴

∴
 ,∴数列{an}是首项为
,∴数列{an}是首项为 ,公比为
,公比为 的等比数列。
的等比数列。(2)由(1)知

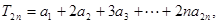

两式相减得:

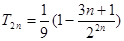
 ,又
,又
当n=1时,9
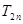 <
<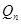 ;
;当n=2时,9
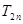 <
<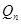 ;
;当n≥3时,22n=[(1+1)n]2=(
 )2>(2n+1)2,∴9
)2>(2n+1)2,∴9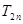 >
>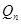 .
.
练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
 ,从
,从 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点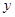 轴的垂线,交
轴的垂线,交 ,设
,设

 的通项公式;
的通项公式;  ,数列
,数列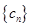 的前
的前 项和为
项和为 ,试比较
,试比较 的大小
的大小 ;
; ,数列
,数列 的前
的前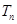 ,试证明:
,试证明: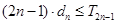

 ,
, ,
, ,
, ,…,则
,…,则 是这个数列的
是这个数列的  层台阶,若每次可上一层或两层,设上法总数为
层台阶,若每次可上一层或两层,设上法总数为 ,则下列猜想正确的是
,则下列猜想正确的是




 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的
 都有
都有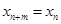 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时,
时, 的周期数列;当
的周期数列;当 时,
时, 是周期为
是周期为 的周期数列。设数列
的周期数列。设数列 满足
满足
 .
. 的周期数列,则常数
的周期数列,则常数 的值是 ;
的值是 ; ,若
,若 ,则
,则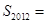 .
. 中,
中, ,
, ,则数列通项
,则数列通项 __________
__________ ,对任意的
,对任意的 满足
满足 ,且
,且 ,那么
,那么 等于
等于 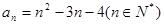 ,则a4等于( ).
,则a4等于( ).