题目内容
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,且椭圆C与椭圆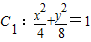 的离心率相同,过F1的直线交椭圆C于A,B两点,且△ABF2的周长为
的离心率相同,过F1的直线交椭圆C于A,B两点,且△ABF2的周长为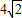 ,那么椭圆C的方程为 .
,那么椭圆C的方程为 .
【答案】分析:根据题意,△ABF2的周长为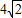 ,即BF2+AF2+BF1+AF1=
,即BF2+AF2+BF1+AF1=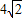 ,结合椭圆的定义,有4a=
,结合椭圆的定义,有4a=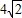 ,即可得a的值;又由椭圆的离心率,可得c的值,进而可得b的值;由椭圆的焦点在x轴上,可得椭圆的方程.
,即可得a的值;又由椭圆的离心率,可得c的值,进而可得b的值;由椭圆的焦点在x轴上,可得椭圆的方程.
解答:解:根据题意,△ABF2的周长为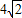 ,即BF2+AF2+BF1+AF1=
,即BF2+AF2+BF1+AF1=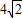 ;
;
根据椭圆的性质,有4a=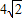 ,即a=
,即a=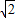 ;
;
椭圆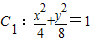 的离心率为
的离心率为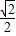 ,即
,即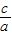 =
=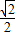 ,则a=
,则a=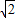 c,
c,
将a=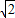 c,代入可得,c=1,则b2=a2-c2=1;
c,代入可得,c=1,则b2=a2-c2=1;
则椭圆的方程为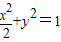 ;
;
故答案为: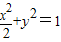
点评:本题考查椭圆的性质,此类题型一般与焦点三角形联系,难度一般不大;注意结合椭圆的基本几何性质解题即可.
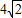 ,即BF2+AF2+BF1+AF1=
,即BF2+AF2+BF1+AF1=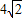 ,结合椭圆的定义,有4a=
,结合椭圆的定义,有4a=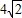 ,即可得a的值;又由椭圆的离心率,可得c的值,进而可得b的值;由椭圆的焦点在x轴上,可得椭圆的方程.
,即可得a的值;又由椭圆的离心率,可得c的值,进而可得b的值;由椭圆的焦点在x轴上,可得椭圆的方程.解答:解:根据题意,△ABF2的周长为
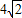 ,即BF2+AF2+BF1+AF1=
,即BF2+AF2+BF1+AF1=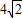 ;
;根据椭圆的性质,有4a=
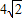 ,即a=
,即a=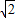 ;
;椭圆
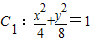 的离心率为
的离心率为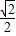 ,即
,即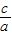 =
=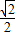 ,则a=
,则a=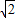 c,
c,将a=
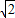 c,代入可得,c=1,则b2=a2-c2=1;
c,代入可得,c=1,则b2=a2-c2=1;则椭圆的方程为
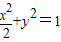 ;
;故答案为:
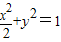
点评:本题考查椭圆的性质,此类题型一般与焦点三角形联系,难度一般不大;注意结合椭圆的基本几何性质解题即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是