题目内容
在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+ a4+ a5="(" )
| A.33 | B.72 | C.84 | D.189 |
C
解析试题分析:在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21
故3+3q+3q2=21,∴q=2
∴a3+a4+a5=21×22=84,故选C。
考点:本题主要考查等比数列的通项公式及性质.
点评:要理解和记忆好等比数列的通项公式,并能熟练灵活的应用。

练习册系列答案
相关题目
已知数列{an}满足a1=1,a2=1,an+1=|an-an-1|(n≥2),则该数列前2011项的和S2011等于( )
| A.1341 | B.669 | C.1340 | D.1339 |
已知数列 满足
满足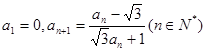 ,则
,则 等于( )
等于( )
A.0 | B.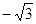 | C.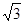 | D. |
在8×8棋盘的64个方格中,共有由整数个小方格组成的大小或位置不同的正方形的个数为
| A.64 | B.128 | C.204 | D.408 |
已知数列 满足:
满足: ,
, ,当且仅当
,当且仅当 时
时 最小,则实数
最小,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.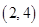 | D. |
在数列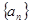 中,如果存在常数
中,如果存在常数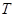
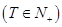 ,使得
,使得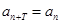 对于任意正整数
对于任意正整数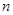 均成立,那么就称数列
均成立,那么就称数列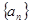 为周期数列,其中
为周期数列,其中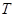 叫做数列
叫做数列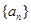 的周期. 已知数列
的周期. 已知数列 满足
满足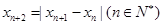 ,若
,若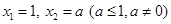 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和
的前2012项的和 为( )
为( )
| A.1339+a | B.1340+a | C.1341+a | D.1342+a |
 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是



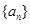 满足
满足 ,则
,则 的最小值是
的最小值是  中,
中, ,
, ,
, ,则
,则
 = .
= .