题目内容
已知函数f（x）=1+2x-tanx，
，则f（x）的单调减区间是________．
分析：求出函数的导数，令导数小于0，求出函数的单调减区间，求出与
的交集即可．解答：∵f（x）=2x-tanx，
∴
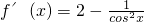=2-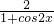
令f′（x）=0得1+cos2x=1
又x∈
，得x=
，故当x∈
时导数为正，当x∈
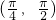时，导数为负，故函数在
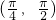上减，因为，所以函数f（x）的单调减区间是：
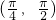．故答案为：
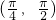．点评：利用导数求函数的单调减区间的关键是正确求出函数的导数，根据导数小于0判断是解题的关键，本题中正切函数的导数求导方法是：先切化弦再利用商的导数法则求导．考查计算能力．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知函数f（x）=
，g（x）=1+
，若f（x）＞g（x），则实数x的取值范围是（ ）
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、（-∞，-1）∪（0，1） | ||||
B、(-∞，-1)∪(0，
| ||||
C、(-1，0)∪(
| ||||
D、(-1，0)∪(0，
|