题目内容
函数f(x)=logax的自变量与函数值的一组近似值为
(1)写出f(x)的解析式.
(2)若A,B是y=f(x)图象上两点,其横坐标分别为a和a+4,直线l:x=a+2与y=f(x)的图象交于点C,与直线AB交于D.求D的坐标和当△ABC面积大于lg2时a的取值范围.
| x | 2 | 3 | 4 | 5 |
| y | 0.3010 | 0.4771 | 0.6020 | 0.6990 |
(2)若A,B是y=f(x)图象上两点,其横坐标分别为a和a+4,直线l:x=a+2与y=f(x)的图象交于点C,与直线AB交于D.求D的坐标和当△ABC面积大于lg2时a的取值范围.
分析:(1)由表中数据代入可得a的值
(2)先画出函数图象,由对数函数图象性质及梯形性质,即可得D点坐标,最后利用梯形面积公式计算△ABC面积,由面积大于lg2解不等式即可得a的范围
(2)先画出函数图象,由对数函数图象性质及梯形性质,即可得D点坐标,最后利用梯形面积公式计算△ABC面积,由面积大于lg2解不等式即可得a的范围
解答:解:(1)∵lg2≈0.3010,lg3≈0.4771,lg4=2lg2≈0.6020
∴a=10
∴f(x)=lgx
(2)如图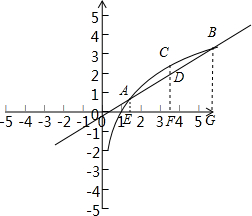 :E、F、G分别为(a,0),(a+2,0),(a+4,0),且F恰为EG中点
:E、F、G分别为(a,0),(a+2,0),(a+4,0),且F恰为EG中点
在直角梯形AEGB中,FD=
=
=lg
∴D的坐标为(a+2,lg
)
∵S△ABC=S梯形AEFC+S梯形CFGB-S梯形AEFD-S梯形DFGB
=
[lga+lg(a+2)]×2+
[lg(a+2)+lg(a+4)]×2-
[lga+lg
]×2-
[lg
+lg(a+4)]×2
=lg[a(a+2)]+lg[(a+2)(a+4)]-lg[a(
)]-lg[(a+4)
]
=lg
=lg
由lg
>lg2
得
>2
解得a>0
∴a=10
∴f(x)=lgx
(2)如图
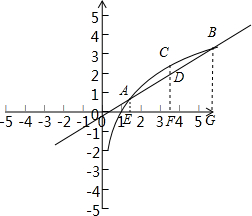 :E、F、G分别为(a,0),(a+2,0),(a+4,0),且F恰为EG中点
:E、F、G分别为(a,0),(a+2,0),(a+4,0),且F恰为EG中点在直角梯形AEGB中,FD=
| AE+GB |
| 2 |
| lga+lg(a+4) |
| 2 |
| a(a+4) |
∴D的坐标为(a+2,lg
| a(a+4) |
∵S△ABC=S梯形AEFC+S梯形CFGB-S梯形AEFD-S梯形DFGB
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a(a+4) |
| 1 |
| 2 |
| a(a+4) |
=lg[a(a+2)]+lg[(a+2)(a+4)]-lg[a(
| a(a+4) |
| a(a+4) |
=lg
| a×(a+2)2×(a+4) |
| a×(a+4)×a×(a+4) |
=lg
| (a+2)2 |
| a×(a+4) |
由lg
| (a+2)2 |
| a×(a+4) |
得
| (a+2)2 |
| a×(a+4) |
解得a>0
点评:本题考查了对数函数的图象和性质,对数运算性质,数形结合的思想方法

练习册系列答案
相关题目
已知函数f(x)=log -
(x2-ax+3a)在[2,+∞)上是减函数,则实数a的范围是( )
| 1 |
| 2 |
| A、(-∞,4] |
| B、(-4,4] |
| C、(0,12) |
| D、(0,4] |