题目内容
已知函数f(x)=ex g(x),其中g(x)=ax2﹣2x﹣2.
g(x),其中g(x)=ax2﹣2x﹣2.
(1)若存在x∈R,使得g(x)>0成立,求实数a的取值范围;
(2)求函数y=f(|sinx|)的值域.
 g(x),其中g(x)=ax2﹣2x﹣2.
g(x),其中g(x)=ax2﹣2x﹣2. (1)若存在x∈R,使得g(x)>0成立,求实数a的取值范围;
(2)求函数y=f(|sinx|)的值域.
解:(1)存在x∈R,使得g(x)>0,
即存在x∈R,使得ax2﹣2x﹣2>0,
当a>0时,满足要求;
当a=0时,满足要求;
当a<0时,△>0,解得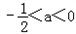
综上得,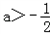
(2)f(x)=exg(x)=ex(ax2﹣2x﹣2)
∴f'(x)=(ex)' (ax2﹣2x﹣2)+ex
(ax2﹣2x﹣2)+ex (ax2﹣2x﹣2)'
(ax2﹣2x﹣2)'
=ex (ax2﹣2x﹣2)+ex
(ax2﹣2x﹣2)+ex (2ax﹣2)
(2ax﹣2)
=ex [ax2+(2a﹣2)x﹣4]
[ax2+(2a﹣2)x﹣4]
设|sinx|=t,(0≤t≤1),则转化为求函数y=f(t),(0≤t≤1)的值域.
当a=0时,f'(x)=﹣2ex(x+2)<0,此时函数f(t)在[0,1]上为减函数,
∴函数f(t)的值域为[f(1),f(0)],即[(a﹣4)e,﹣2]
当a<0时,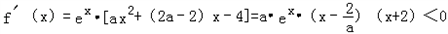
此时函数f(t)在[0,1]上为减函数,
∴函数f(t)的值域为[f(1),f(0)],即[(a﹣4)e,﹣2]
当a>0时,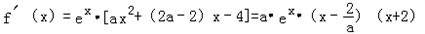
令f'(x)=0,解得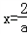 或x=﹣2(舍).
或x=﹣2(舍).
当x变化时,f(x)与f'(x)的变化情况如下表:
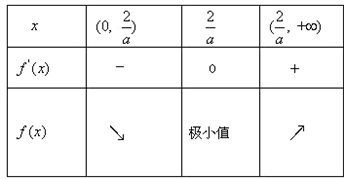
若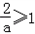 ,即0<a≤2时,函数f(t)在[0,1]上为减函数.
,即0<a≤2时,函数f(t)在[0,1]上为减函数.
∴函数f(t)的值域为[f(1),f(0)],即[(a﹣4)e,﹣2]
若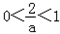 ,即a>2时,函数f(t)在
,即a>2时,函数f(t)在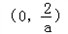 上递减,在
上递减,在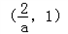 上递增
上递增
∴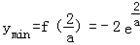
函数f(t)在[0,1]上的最大值为f(0)与f(1)中的较大者
∵f(0)=﹣2,f(1)=(a﹣4)e,
∴f(1)﹣f(0)=(a﹣4)e+2
∴当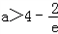 时,f(1)>f(0),
时,f(1)>f(0),
此时ymax=f(1)=(a﹣4)e;
当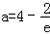 时,f(1)=f(0),此时ymax=f(0)=f(1)=﹣2;
时,f(1)=f(0),此时ymax=f(0)=f(1)=﹣2;
当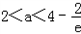 时,f(1)<f(0),此时ymax=f(0)=﹣2
时,f(1)<f(0),此时ymax=f(0)=﹣2
综上,当a?2时,函数f(|sinx|)的值域为[(a﹣4)e,﹣2];
当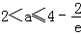 时,函数f(|sinx|)的值域为
时,函数f(|sinx|)的值域为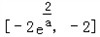 ;
;
当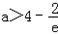 时,函数f(|sinx|)的值域为
时,函数f(|sinx|)的值域为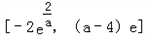 .
.
即存在x∈R,使得ax2﹣2x﹣2>0,
当a>0时,满足要求;
当a=0时,满足要求;
当a<0时,△>0,解得
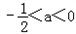
综上得,
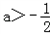
(2)f(x)=exg(x)=ex(ax2﹣2x﹣2)
∴f'(x)=(ex)'
 (ax2﹣2x﹣2)+ex
(ax2﹣2x﹣2)+ex (ax2﹣2x﹣2)'
(ax2﹣2x﹣2)'=ex
 (ax2﹣2x﹣2)+ex
(ax2﹣2x﹣2)+ex (2ax﹣2)
(2ax﹣2)=ex
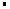 [ax2+(2a﹣2)x﹣4]
[ax2+(2a﹣2)x﹣4]设|sinx|=t,(0≤t≤1),则转化为求函数y=f(t),(0≤t≤1)的值域.
当a=0时,f'(x)=﹣2ex(x+2)<0,此时函数f(t)在[0,1]上为减函数,
∴函数f(t)的值域为[f(1),f(0)],即[(a﹣4)e,﹣2]
当a<0时,
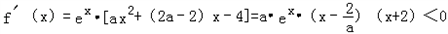
此时函数f(t)在[0,1]上为减函数,
∴函数f(t)的值域为[f(1),f(0)],即[(a﹣4)e,﹣2]
当a>0时,
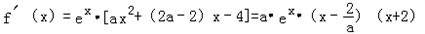
令f'(x)=0,解得
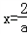 或x=﹣2(舍).
或x=﹣2(舍).当x变化时,f(x)与f'(x)的变化情况如下表:

若
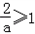 ,即0<a≤2时,函数f(t)在[0,1]上为减函数.
,即0<a≤2时,函数f(t)在[0,1]上为减函数.∴函数f(t)的值域为[f(1),f(0)],即[(a﹣4)e,﹣2]
若
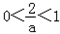 ,即a>2时,函数f(t)在
,即a>2时,函数f(t)在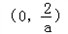 上递减,在
上递减,在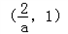 上递增
上递增∴
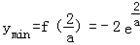
函数f(t)在[0,1]上的最大值为f(0)与f(1)中的较大者
∵f(0)=﹣2,f(1)=(a﹣4)e,
∴f(1)﹣f(0)=(a﹣4)e+2
∴当
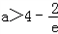 时,f(1)>f(0),
时,f(1)>f(0),此时ymax=f(1)=(a﹣4)e;
当
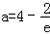 时,f(1)=f(0),此时ymax=f(0)=f(1)=﹣2;
时,f(1)=f(0),此时ymax=f(0)=f(1)=﹣2;当
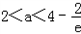 时,f(1)<f(0),此时ymax=f(0)=﹣2
时,f(1)<f(0),此时ymax=f(0)=﹣2综上,当a?2时,函数f(|sinx|)的值域为[(a﹣4)e,﹣2];
当
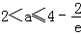 时,函数f(|sinx|)的值域为
时,函数f(|sinx|)的值域为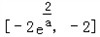 ;
;当
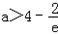 时,函数f(|sinx|)的值域为
时,函数f(|sinx|)的值域为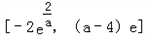 .
.
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目