题目内容
(本小题满分13分)
已知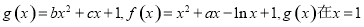 处的切线为
处的切线为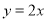
(I)求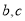 的值;
的值;
(II)若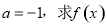 的极值;
的极值;
(III)设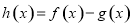 ,是否存在实数
,是否存在实数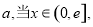 (
(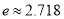 ,为自然常数)时,函数
,为自然常数)时,函数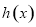 的最小值为3.
的最小值为3.
(I) ;(II)
;(II) ;(III)
;(III) .
.
【解析】
试题分析:(1)根据 的解析式求出函数的导函数,由条件可得
的解析式求出函数的导函数,由条件可得 ,
, ,进而可得出
,进而可得出 (2)根据题意可确定函数的解析式
(2)根据题意可确定函数的解析式 ,进而求导、列表判断函数的单调性,得出函数的极值;(3)列出函数的解析式求出导数,然后对
,进而求导、列表判断函数的单调性,得出函数的极值;(3)列出函数的解析式求出导数,然后对 分类讨论结合函数的单调性判断是否存在这样的值..
分类讨论结合函数的单调性判断是否存在这样的值..
试题解析:(Ⅰ)  在
在 处的切线为
处的切线为
所以 ,即
,即
又在 处
处 ,所以
,所以
所以 ,可得
,可得
所以 3分
3分
(Ⅱ)  时
时 ,定义域为
,定义域为

|
|
|
|
|
|
|
|
|
| 极小值 |
|
可以看出,当 时,函数
时,函数 有极小值
有极小值 8分
8分
(Ⅲ) 因为 ,
,
所以
假设存在实数 ,使
,使 有最小值
有最小值 ,
,
 9分
9分
①当 时,
时, ,所以
,所以
 在
在 上单调递减,
上单调递减, (舍去) 10分
(舍去) 10分
②当 时,
时,
(i)当 时,
时, ,
, 在
在 上恒成立
上恒成立
所以 在
在 上单调递减,
上单调递减, (舍去) 11分
(舍去) 11分
(ii)当 时,
时,  ,当
,当 时,
时, 所以
所以 在
在 上递减
上递减
当 时
时 ,
, 在
在 上递增
上递增
所以,  12分
12分
所以 满足条件, 综上,存在
满足条件, 综上,存在 使
使 时
时 有最小值
有最小值 13分
13分
考点:函数及其导数性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目












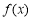 满足
满足 ,当
,当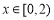 时,
时, 函数
函数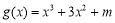 .若
.若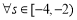 ,
,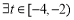 ,不等式
,不等式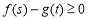 成立,则实数m的取值范围是( )
成立,则实数m的取值范围是( )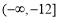 (B)
(B)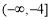
 (D)
(D)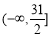
 分别为双曲线
分别为双曲线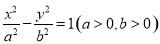 的左,右焦点,P为双曲线右支上的一点,且
的左,右焦点,P为双曲线右支上的一点,且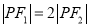 .若
.若 为等腰三角形,则该双曲线的离心率为_________.
为等腰三角形,则该双曲线的离心率为_________.
 的部分图象如图所示,则在
的部分图象如图所示,则在 上,下列函数中与
上,下列函数中与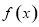 的单调性不同的是
的单调性不同的是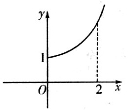
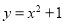 B.
B. 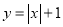
 D.
D. 
 在
在 上恒为单调递增函数,则实数
上恒为单调递增函数,则实数 的取值范围________.
的取值范围________. 的零点所在的大致区间是
的零点所在的大致区间是 B.
B.  C.
C.  D.
D. 
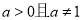 时,函数
时,函数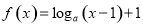 的图像恒过点A,若点A在直线
的图像恒过点A,若点A在直线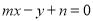 上,则
上,则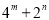 的最小值为_________.
的最小值为_________. 满足
满足 ,则
,则 的最大值为
的最大值为