题目内容
关于函数f(x)=4sin(2x+
)(x∈R)有以下命题:①由f(x1)=f(x2)=0有x1-x2必是π的整数倍;②y=f(x)的表达式可改写为y=4cos(2x-
);③y=f(x)的图象关于点(-
,0)对称;④y=f(x)的图象关于直线x=-
对称.
其中正确的命题是___________.
解析:对于①,f(x1)=4sin(2x1+)=0,
f(x2)=4sin(2x2+)=0,
∴2x1+=k1π,2x2+=k2π.
∴x1=
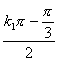,x2=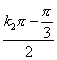
.
∴x1-x2=
(k1π-
-k2π+
)=
.
k1-k2不一定为偶数,∴x1-x2不一定为π的整数倍.
∴①错误.
对于②,y=4sin(2x+
)=4cos(
-2x-
)=4cos(
-2x)=4cos(2x-
),
∴②正确.
对于③,令2x+
=kπ,∴2x=kπ-
.
∴x=
-
.
令k=0,∴一个对称中心为(-
,0),③正确.
对于④,令2x+
=kπ+
,
∴2x=kπ+
.
∴x=
,故④错误.
故选②③.
答案:②③
练习册系列答案
相关题目
关于函数f(x)=lg
(x≠0)，有下列命题：（1）其图象关于y轴对称；（2）当x＞0时，f（x）是增函数，当x＜0时，f（x）是减函数；（3）f（x）在区间（-1，0）和（1，+∞）上均为增函数；（4）f（x）的最小值是lg2．其中所有正确的结论序号是（ ）
| x2+1 |
| |x| |
| A、（1）（2）（3） |
| B、（1）（2）（4） |
| C、（1）（3）（4） |
| D、（2）（3）（4） |