题目内容
已知f(x)=2cos2x+ sin2x+a (a∈R,a为常数)
sin2x+a (a∈R,a为常数)
(Ⅰ) 若x∈R,求f(x)的单调增区间;
(Ⅱ) 若x∈[0, ]时,f(x)的最大值为4,并求此时f(x)的最小值.
]时,f(x)的最大值为4,并求此时f(x)的最小值.
解:(Ⅰ)f(x)=2cos2x+ sin2x+a
sin2x+a
=cos2x+ sin2x+a+1
sin2x+a+1
=2 sin(2x+ )+a+1,
)+a+1,
∴f(x)的单调增区间为[kπ- ,kπ+
,kπ+ ],k∈Z.…(6分)
],k∈Z.…(6分)
(Ⅱ)∵x∈[0, ]时,f(x)的最大值为4
]时,f(x)的最大值为4
∴ ≤2x+
≤2x+ =u≤
=u≤
∴f(x)在[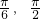 ]单调递增,在(
]单调递增,在( ]单调递减
]单调递减
∴f(x)max=2+a+1=4,
∴a=1.…(9分)
故:当2x+ =
= ,即
,即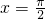 时,
时,
f(x)min=2×( )+1+1=1…(12分)
)+1+1=1…(12分)
分析:(1)利用降幂公式cos2x=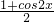 和辅助角公式可将f(x)=2cos2x+
和辅助角公式可将f(x)=2cos2x+ sin2x+a 转化为f(x)=2 sin(2x+
sin2x+a 转化为f(x)=2 sin(2x+ )+a+1再类比正弦函数的单调性可得不等式2kπ-
)+a+1再类比正弦函数的单调性可得不等式2kπ- ≤2x
≤2x ≤2kπ
≤2kπ ,k∈z的解集即为f(x)的单调增区间.
,k∈z的解集即为f(x)的单调增区间.
(2)可将2x 看做一个整体u然后判断出f(x)在u的范围上的单调性求出f(x)的最大值再根据f(x)的最大值为4可求出a进而求出最小值.
看做一个整体u然后判断出f(x)在u的范围上的单调性求出f(x)的最大值再根据f(x)的最大值为4可求出a进而求出最小值.
点评:本题主要考察了函数y=Asin(wx+∅)+k的单调性,属中等难度的试题.解题的关键是牢记函数y=Asin(wx+∅)+k的单调区间的求解和在某一区间上单调性的判断!
 sin2x+a
sin2x+a=cos2x+
 sin2x+a+1
sin2x+a+1=2 sin(2x+
 )+a+1,
)+a+1,∴f(x)的单调增区间为[kπ-
 ,kπ+
,kπ+ ],k∈Z.…(6分)
],k∈Z.…(6分)(Ⅱ)∵x∈[0,
 ]时,f(x)的最大值为4
]时,f(x)的最大值为4∴
 ≤2x+
≤2x+ =u≤
=u≤
∴f(x)在[
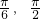 ]单调递增,在(
]单调递增,在( ]单调递减
]单调递减∴f(x)max=2+a+1=4,
∴a=1.…(9分)
故:当2x+
 =
= ,即
,即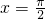 时,
时,f(x)min=2×(
 )+1+1=1…(12分)
)+1+1=1…(12分)分析:(1)利用降幂公式cos2x=
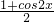 和辅助角公式可将f(x)=2cos2x+
和辅助角公式可将f(x)=2cos2x+ sin2x+a 转化为f(x)=2 sin(2x+
sin2x+a 转化为f(x)=2 sin(2x+ )+a+1再类比正弦函数的单调性可得不等式2kπ-
)+a+1再类比正弦函数的单调性可得不等式2kπ- ≤2x
≤2x ≤2kπ
≤2kπ ,k∈z的解集即为f(x)的单调增区间.
,k∈z的解集即为f(x)的单调增区间.(2)可将2x
 看做一个整体u然后判断出f(x)在u的范围上的单调性求出f(x)的最大值再根据f(x)的最大值为4可求出a进而求出最小值.
看做一个整体u然后判断出f(x)在u的范围上的单调性求出f(x)的最大值再根据f(x)的最大值为4可求出a进而求出最小值.点评:本题主要考察了函数y=Asin(wx+∅)+k的单调性,属中等难度的试题.解题的关键是牢记函数y=Asin(wx+∅)+k的单调区间的求解和在某一区间上单调性的判断!

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目