题目内容
在钝角△ABC中,已知AB=
,AC=1,∠B=30°,则△ABC的面积是( )
| 2 |
分析:在钝角△ABC中,有正弦定理求得 sinC,再由 b边不是最大边可得AB或BC为最大边,求出角 C,根据三角形的内角和公式求出A,由此求得△ABC的面积
×AB×ACsinA 的值.
| 1 |
| 2 |
解答:解:在钝角△ABC中,有正弦定理可得
=
,即
=
,求得 sinC=
.
再由 b边不是最大边可得AB为最大边,或者BC为最大边.
若AB为最大边,则 C=135°,∴A=15°,∴sin15°=
=
.
∴△ABC的面积是
×AB×ACsinA=
×
×1×
=
,
若BC为最大边,则C=45°,A=105°,
sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
,
∴△ABC的面积是
×AB×ACsinA=
×
×1×
=
.
故选D.
| AB |
| sinC |
| AC |
| sinB |
| ||
| sinC |
| 1 |
| sin30° |
| ||
| 2 |
再由 b边不是最大边可得AB为最大边,或者BC为最大边.
若AB为最大边,则 C=135°,∴A=15°,∴sin15°=
|
| ||||
| 4 |
∴△ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||||
| 4 |
| ||
| 4 |
若BC为最大边,则C=45°,A=105°,
sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
| ||||
| 4 |
∴△ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||||
| 4 |
| ||
| 4 |
故选D.
点评:本题主要考查正弦定理的应用,三角形的内角和公式,以及大边对大角,属于中档题.

练习册系列答案
相关题目
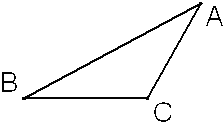 如图,在钝角△ABC中,已知三条边a,b,c和三个角A,B,C,证明:a=bcosC+ccosB.
如图,在钝角△ABC中,已知三条边a,b,c和三个角A,B,C,证明:a=bcosC+ccosB. ,
, ,则最大边
,则最大边 的取值范围是 。
的取值范围是 。 ,
, ,则最大边
,则最大边 的取值范围是
的取值范围是  , AC=1,∠A=30°,则△ABC的面积是
, AC=1,∠A=30°,则△ABC的面积是  B.
B. C.
C. D.
D.