题目内容
如图所示:边长为2的正方形ABCD和高为2的直角梯形ADEF所在的平面互相垂直且
![]() .
.

(1) 求BD和面BEF所成的角的余弦;
(2) 线段EF上是否存在点P使过P、A、C三点的平面和直线DB垂直,若存在,求EP与PF的比值;若不存在,说明理由.
解:(1)因为AC、AD、AB两两垂直,建立如图坐标系,
则B(2,0,0),D(0,0,2),E(1,1,2),F(2,2,0),则
![]()
 设平面BEF的法向量为n=(x,y,z),则-x+y+2z=0,y=0,则可取n=(2,0,1),
设平面BEF的法向量为n=(x,y,z),则-x+y+2z=0,y=0,则可取n=(2,0,1),
∴向量![]() 和n=(2,0,1)所成角的余弦为
和n=(2,0,1)所成角的余弦为
即BD和面BEF所成的角的余弦![]()

练习册系列答案
相关题目
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=![]() ,ED//AF且∠DAF=90°。
,ED//AF且∠DAF=90°。
(1)求BD和面BEF所成的角的余弦;
|
|
 如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2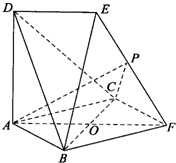 如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE= 如图所示,边长为2的等边△
如图所示,边长为2的等边△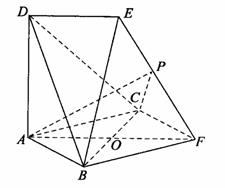
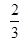 ,则阴影区域的面积为( )
,则阴影区域的面积为( )
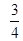 B.
B.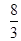 C.
C.