题目内容
设二次函数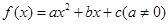 满足条件:①当
满足条件:①当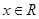 时,
时,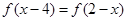 ,且
,且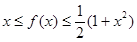 ;②
;②
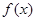 在
在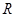 上的最小值为
上的最小值为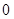 。(1)求
。(1)求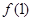 的值及
的值及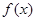 的解析式;(2)若
的解析式;(2)若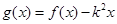 在
在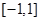 上是单调函数,求
上是单调函数,求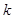 的取值范围;(3)求最大值
的取值范围;(3)求最大值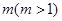 ,使得存在
,使得存在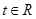 ,只要
,只要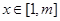 ,就有
,就有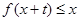 。
。
【答案】
(1) ∵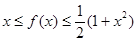 在
在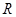 上恒成立,∴
上恒成立,∴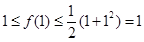
即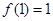 ……………(1分)
……………(1分)
∵ ,∴函数图象关于直线
,∴函数图象关于直线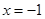 对称,
对称,
∴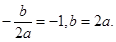 ……………(2分)
……………(2分)
∵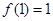 ,∴
,∴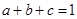
又∵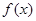 在
在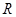 上的最小值为
上的最小值为 ,∴
,∴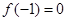 ,即
,即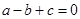 ,……………(3分)
,……………(3分)
由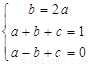 解得
解得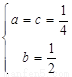 ,∴
,∴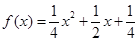 ;……………(4分)
;……………(4分)
(2)∵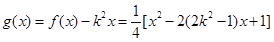 ,
,
∴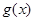 对称轴方程为
对称轴方程为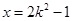 ,……………(5分)
,……………(5分)
∵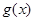 在
在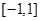 上是单调函数,∴
上是单调函数,∴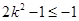 或
或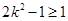 ,……………(7分)
,……………(7分)
∴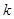 的取值范围是
的取值范围是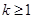 或
或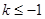 或
或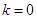 。……………(8分)
。……………(8分)
(3)∵当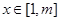 时,
时,
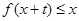 恒成立,∴
恒成立,∴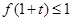 且
且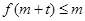 ,
,
由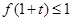 得
得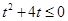 ,解得
,解得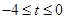 ……………(9分)
……………(9分)
由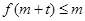 得:
得: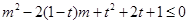 ,
,
解得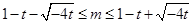 ,……………(10分)
,……………(10分)
∵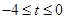 ,∴
,∴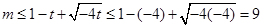 ,……………(11分)
,……………(11分)
当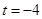 时,对于任意
时,对于任意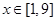 ,恒有
,恒有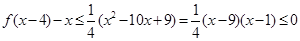 ,
,
∴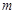 的最大值为
的最大值为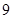 .……………(12分)
.……………(12分)
另解: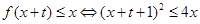 且
且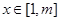
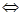
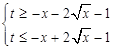 在
在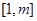 上恒成立
上恒成立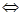
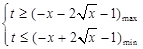
∵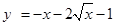 在
在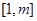 上递减,∴
上递减,∴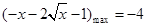 ,
,
∵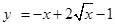 在
在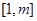 上递减,∴
上递减,∴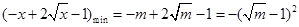
∴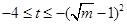 ,∴
,∴ ,
,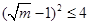 ,∵
,∵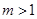 ,∴
,∴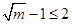 ,
,
∴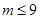 ,∴
,∴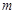 的最大值为
的最大值为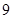
【解析】略

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 满足条件:
满足条件: ;②函数
;②函数 的图象与直线
的图象与直线 只有一个公共点。
只有一个公共点。 时恒成立,求实数
时恒成立,求实数 的取值范围。
的取值范围。 满足条件:
满足条件: ;②函数
;②函数 的图象与直线
的图象与直线 只有一个公共点。
只有一个公共点。 时恒成立,求实数
时恒成立,求实数 的取值范围。
的取值范围。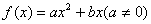 满足条件:
满足条件: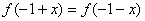 ;②函数
;②函数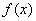 的图象与直线
的图象与直线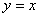 只有一个公共点。
只有一个公共点。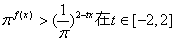 时恒成立,求实数
时恒成立,求实数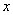 的取值范围。
的取值范围。