Question

14．如图所示几何体为正方体ABCD-A₁B₁C₁D₁截去三棱锥B₁-A₁BC₁后所得，点M为A₁C₁的中点．
（1）求证：CM∥平面A₁BD；
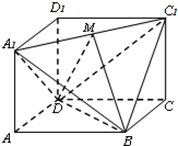
（2）求二面角B-DM-C的余弦值．

Answer 1

分析 （1）根据线面平行的判定定理即可证明CM∥平面A₁BD；
（2）求出平面的法向量，利用向量法即可求二面角B-DM-C的余弦值．

解答 证明：（1）连接AC交BD于O，连接CM，OA₁，
则O是AC的中点，
则∵M为A₁C₁的中点，
∴A₁M∥OC，且A₁M=OC，
即四边形OCMA₁是平行四边形，
则CM∥OA₁，
∵CM?平面A₁BD，OA₁?平面A₁BD；
∴CM∥平面A₁BD；
（2）建立以D为原点，DA，DC，DD₁为坐标轴的坐标系如图；
设正方体的棱长为1，
则B（1，1，0），C（0，1，0），A₁（1，0，1），C₁（0，1，1，），
则M（$\frac{1}{2}$，$\frac{1}{2}$，1），
则$\overrightarrow{DB}$=（1，1，0），$\overrightarrow{DM}$=（$\frac{1}{2}$，$\frac{1}{2}$，1），$\overrightarrow{DC}$=（0，1，0），
设平面BDM的法向量为$\overrightarrow{m}$=（x，y，z），
则由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DB}=x+y=0}\\{\overrightarrow{m}•\overrightarrow{DM}=\frac{1}{2}x+\frac{1}{2}y+z=0}\end{array}\right.$，
令y=2，则x=-2，z=0，
即$\overrightarrow{m}$=（-2，2，0），
设平面BDC的法向量为$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DM}=\frac{1}{2}x+\frac{1}{2}y+z=0}\\{\overrightarrow{n}•\overrightarrow{DC}=y=0}\end{array}\right.$，
令x=-2，则z=1，
即$\overrightarrow{n}$=（-2，0，1），
则cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{4}{\sqrt{8}×\sqrt{5}}$=$\frac{\sqrt{10}}{5}$，
即二面角B-DM-C的余弦值是$\frac{\sqrt{10}}{5}$．

点评 本小题主要考查立体几何的相关知识，具体涉及到线面平行的判定、二面角的求法及空间向量在立体几何中的应用．本小题对考生的空间想象能力与运算求解能力有较高要求．